The problem of truth and the ontological foundation of cognition*

F.T. Arecchi

University of Firenze

and

Istituto Nazionale di Ottica Applicata

arecchi@ino.it

1-Introduction –Plan of the work

A cognitive task corresponds to asking two kinds of questions: HOW? WHY? , and answering respectively by descriptions or explanations.

Modern science is built upon a self limitation, that is, “don’t try the essences (natures) but limit to quantitative appearances” (letter by G. Galilei to M. Welser, 1612) which cuts off ontological investigations from the scientific program.

Each separate appearance is extracted by a suitable measuring apparatus and ordered as an element of a metric space ,a whole is a collection of numbers corresponding to the measures of the appearances; whence the success of mathematics in scientific description. Regularities suggest stable correlations (the laws) with a validity domain established by falsification methods. The working language is “formal” and the truth of a proposition is its correspondence to the language rules.

However, there remains two open problems, namely, i) the inverse reconstruction : how we organize appearances into coherent bodies and ii) the completeness of the direct approach: how, in the jargon of the Gestalt psychology, we select perceptual saliencies by picking up only a few among the many appearances which occur to our experience and consider these few ones as meaningful.

The concept of meaning does not occur in descriptions but only in explanations. It appears in science as a meta-principle, as e.g. Darwinian fitness, but it is outside the set of rules which characterizes a formal language. We might try to extend the language by including the meta-rules, but it would be an endless effort. The pretension of a formal language to provide a complete description is incompatible with its coherence, unless one postulates a finitistic universe where all events and the corresponding evaluation procedures require a finite number of steps.

These problems have been dealt with by two opposite investigation lines, loosely corresponding to the so called “analytic” and “continental” philosophers. The former ones identify philosophy with descriptions, reducing all problems to questions within a formal language. The second ones see cognition as intentional, that is, pointing at something but they leave open the question whether the cognitive features are outside or only inside our mind.

The scientific endeavour seems to be within the first line and we have seen the development of different sciences, each one corresponding to a different group of descriptions, selected by picking up limited of measuring procedures and hence limited sets of appearances. On the other hand, in recent years holistic scientific approaches have been based on nonlinear dynamics. In these approaches the different dynamical variables, or degrees of freedom ,are not taken on equal footing ,by they are organized as a hierarchy. Precisely, a few long standing or most stable variables, called order parameters, slave the fast ones which adjust almost instantly to get in local equilibrium with the slow ones. The onset of a new order parameter occurs by a bifurcation and it is representative of a new reality, thus bifurcations are indicators of the emergence of new realities (H.Haken: synergetics , R.Thom: semiophysics or physics of meanings).If this “synergetic” approach is applied to a system completely specified by a set of variables ,then it is just an good approximation method to reduce the amount of computational work. A complete specification is presumed as a property of “first principle” descriptions which have quantitatively specified all the problems variables .Such a presumption was born with Newtonian mechanics and is proper of the so called TOEs ( theories of everything) .On the contrary, in most experimental situations we deal with macroscopic variables which are selected by the researcher intuition over an open system, that is, a system which is in contact with an environment, so that a complete specification is in principle impossible and we must resort to intuition in order to select relevant features.

All the recent handling techniques of data sets are respectable, provided the data are reliable. Whatever has been the approach (whether of Galileo type, based on a limited set of affections which correspond to salient features, or Newton type , aiming at a complete listing of all the degrees of freedom) the resulting description is within a formalized language (i.e. lists of numbers) and computer scientists have introduced different definitions of complexity to quantify the amount of effort in solving a problem. However the unsolved scientific problem is :how we did arrive at that description ,is it a satisfactory account of “things”. Thom tried to answer the question by putting a parallelism between salient features and our perceptual and linguistic operations. This will found descriptions upon perceptions of objective world features

This new philosophy of nature implies that the holistic approach reflects in a plausible way what goes on in a cognitive process. The formation of coherent perceptions, or cognition, requires the combination of a “bottom-up” line, whereby external stimuli are crucial to induce stable impressions, with a “top-down” line, whereby previous memories regulate the neuron thresholds giving rise to collective synchronized states. This exchange between the two flows is adaptive and is the basis of a true cognition resulting as “adaequatio intellectus et rei”, thus excluding both the passive impression of a detector as well as the solipsism of an autopoietic knowledge.

Thus ,combining complex dynamics and the understanding of neural processes, we arrive at the following conclusions.

1) “Reality” denotes stable events which stimulate coherent perceptions;

2) A dynamic approach considers different levels of reality, each one emerging from its own bifurcation;

3) A description of one level in terms of separate independent points of view (Galileo’s affections) is insufficient and the peculiar bifurcation from where it emerged can be grasped only by a collective (synergetic) description which embeds the different points of view into a single order parameter (indicator of a nature);

4) Truth as adaequatio implies an adaptive, or matching, process ; if each separate description corresponds to a different science, then truth does not refer to a SINGLE science, but implies more than the descriptive stage, hence the level of collective description of a physical event has a corresponding level of holistic perception;

5) Different levels of reality imply mutual relations, causal or teleological, thus the question “WHY” and the corresponding answer (explanation) must span across different levels;

6) As different sciences may refer to the same reality ,albeit from different points of view, observing different realities from the same point of view means attributing to them the same predicate; this is “analogia entis “ which allows to build true (even though incomplete) judgements about realities not directly observed but linked by causal or final bridges.

This is the plan of a program only partly completed. In Sec.2 we summarize the main features of the current computational approach to cognition ,stressing its limitations as compared to a realistic dynamic description of the cognitive processes implying homoclinic chaos and synchronization of the neural signals over large brain areas (Secs.3-5).These sections are the core of the paper and the experimental support is provided by laser experiments. The conjecture that the same dynamics holds for neurons is supported by many neurophysical records, but direct tests on isolated neurons or small groups of coupled neurons are under way. Sec. 6 introduces a distance in perceptual space. Such a distance is conjugated to the time duration of the perceptual tasks, yielding an uncertainty relation (Sec.7) which forbids to localize percepts as points of a space and hence to consider a percept as a set-theoretical object, to be handled by a formal language. Such a prohibition excludes the reducibility of perceptual tasks to computer problems, as done by classical cognitivism ,and introduces adaptiveness as the current strategy to extract reliable information, or truth , from the world.

Finally, Sec.8 is a review of some aspects of nonlinear dynamics which trace a strong parallelism between our perceptions and the relevant features of natural objects and events, confirming that the dynamic approach is not a symbolic construction of reality, but rather a matching between reality and our representations. Thus we can confidently close the gap between science and philosophy of nature, born with the cautious self-limitation of Galileo, which has been very effective in producing a wealth of useful results, even though introducing conceptual and interpretation problems.

2- A turn in cognitive science

A tight correspondence between mental representations and outside events, whatever goes on in the world independently of the observer, is often dubbed as “naïve realism”. Opposed to it, artificial intelligencers have fostered the view point of “construction of reality”, whereby our senses are inputted by atomistic individual sensations and any further correlation among them is the result of a symbolic manipulation operated by the brain.

Classical cognitivism is mentalist, symbolic and functionalist (e.g. Fodor 1981 and Pylyshyn 1986). It assumes that the environment emits physical information (intensities, wavelengths, etc.) which is not significant as such for the cognitive subject, therefore it must be translated by peripheral transducers (retina, cochlea etc.) into neuronal information later processed by the central nervous system through several levels of symbolic mental representations.

Mental representation as a psychological reality is criticized by radical physicalism (Quine, Churchland) and non radical physicalism (Dennett) which accepts mental representations as a descriptive concept not as an objective reality. For classical cognitivists, mental representations are considered to be symbolic (in the sense of symbolic logic) and to be expression of an internal formal language (Fodor’s language of thought, or mentalese). It is hypothesized that there exists a calculus through which these expressions are manipulated by rules. This calculus is implemented physically, hence causally, but causality is restricted to the syntactic structure of expressions. However, functionalism distinguishes the implementation (neuronal hardware) from the symbolic calculus itself.

After such a computational treatment of the input, a projection process takes place resulting in the cognitive construction of a projected world. Phenomenological consciousness is considered as the correlate of this projected world; according to this rule, it is possible to investigate the relationship between consciousness and the computational mind. Moreover, classical cognitivism holds that the computational mind comprises two types of systems:

1) modular peripheral systems which transforms the information provided by the transducers into representations endowed with propositional properties suited to mental calculus (bottom up);

2) central cognitive system non modular (operating top down) and interpretative: since there is no nomological control of its functioning according to some rules, it is not possible to deal with it scientifically.

This second point raises the problem of semantic holism. For Fodor central systems are isotrope, i.e. all beliefs and knowledge are potentially relevant for the interpretation of the module outputs, hence his criticism of the notion of expert systems (Minsky, Winograd, Newel ) since these latter ones consider central systems as if they were modular and specific.

Classical cognitivism implies that what is significant in the environment for the cognitive subject (interaction subject/environment) cannot be derived from the laws of nature and therefore is not part of the scientific psychology because science can only be nomological. A descriptive discipline is not nomological and cannot be considered as a science: this is the thesis of methodological solipsism, for which no constitutive reference to the structures of the external world can be included in a scientific psychology, thus rejecting an ecological approach. This attitude is exemplified by Fodor, who considers the physical reality as the only objective reality. This reality acts causally and nomologically upon the transducers; On the level of central system, only the syntactic form of representation acts casually, and therefore signification cannot be an object of scientific inquiry.

The counter thesis of this work, related to the feature binding approach to perception, is that there exists a natural semiotics in the environment which is not encompassed by classical cognitivism.

Dennett’s point of view is equally criticized as it considers intentional conceptuality to be a predictive strategy i.e. a heuristics which allows to predict how certain systems will behave. Based upon the competence/performance opposition, Dennett’s thesis contends that cognitive systems such as the brain are intentional (they are semantic machines) on the level of kinematic competence (the formal theory of functioning) but that they are actually syntactic machines physiologically i.e. on the dynamic level of performance. In so far as syntax does not determine semantics one may wonder how such system can produce semantics from syntax. Dennett claims that the brain mimics the behaviour of a semantic machine by relying on correspondences between regularities of its internal organization and of its external environment and semantic types. But such a thesis is tenable only if the prime problem of intentionality has been solved.

In these recent years experimental evidence has been provided of feature binding, that is, mutual synchronization of the axonal spike trains in those neurons whose receptive fields are exposed to some feature that we consider as a meaningful event. Laboratory evidence is provided in animals (Singer et al.) by inserting microelectrodes close to the myelin envelope of a single axon in cats or monkeys. In the case of human beings, a nice elaboration of EEG signals has been performed (Rodriguez et al.) showing synchronization of different cortical areas.

Let us consider each neuron as a nonlinear threshold dynamical system yielding as output a spike train whose frequency increases with the above-threshold stimulation. Then the task of synchronizing the receptive fields corresponding to different regions of the same object, which have in general different illumination and hence different inputs, requires modulating the single neuron threshold, in order to adjust its output to that of other neurons involved in the same perception. Such a dynamical operation can be achieved if, besides bottom up signals corresponding to elementary stimuli coming from the transducers, there is a system of top down signals which readjusts the thresholds, based upon some conjectures associated with previous memories(traces of past learning).

Such a feedback system has been hypothesized by Grossberg starting 1980 and called ART (Adaptive Resonance Theory).It is by no means an aposteriori computer elaboration of data already acquired but it involves a dynamical process. In fact, it consists of a matching mechanism which controls the interaction of bottom-up and top-down signals until they reach a stable situation. The mechanism is the sequence of perception – action loops whereby we slowly familiarize with an external environment; it works also in the absence of past memories (tabula rasa ,as in newly born children)and in such a case the very first experiences are crucial to fill the semantic memory with some content. Of course, the adaptation procedure includes changing the memory content in presence of new experiences. Thus we are not in presence of an abstract computational procedure given once for ever but the semantic memory providing the top-down threshold readjustments is modified in course of life. Vidyasagar and other knowledge engineers have called such a cognitive approach PAC (Probably Approximately Correct) knowledge. It seems to provide a sound heuristics but it is just a pragmatic attitude, non nomological ,that is, without a formal scientific ground.

In fact we aim to show the close correspondence that non linear dynamics establishes between events and cognitive facts. We face this endeavour at the most elementary level ,that of the single neuron dynamics and the successive one ,of a collective or coherent pattern pervading a whole neocortical sensory area. However the scientific facts we plan to review are solid enough to claim that both the world events and the brain organisation share similar dynamical features:To rephrase a classical philosopher as Thomas Aquinas we should say that cognitive adaptation leads to

a notion of truth called “adaequatio intellectus et rei”.

The experimental synchronization evidence and the ART conjecture require a mechanism endowed of two characteristics:

1) deterministic chaos is mandatory. Indeed ,the corresponding phase space trajectory is the superposition of a large number of unstable periodic orbits. If each one is coding for a different information, then it is crucial to assure a fast transition from an orbit to another, without energy barriers in between and this would not be possible if the coding elements were stable orbits.

2) among the large crowd of possible chaotic mechanisms, nature must have selected a type of chaos which makes mutual synchronization easy, and yet robust against environmental noise.

Based on these criteria, we present a plausible implementation of neural dynamics in terms of homoclinic chaos. We have explored such a mechanism with reference to laboratory systems as lasers and have built plausible dynamical models. Both experimental and model behaviours mimic very closely the neuron behaviour.

We thus presume that we have uncovered the neurodynamic fundamental behaviour. Synchronization implies space and time correlations of long range. They are usually associated with dynamical phase transitions which characterize the passage from one stable state to another (dynamical bifurcations).

3- Neurodynamics

It is by now firmly established that a holistic perception emerges, out of separate stimuli entering different receptive fields, by synchronizing the corresponding spike trains of neural action potentials [Von der Malsburg, Singer].

We recall that action potentials play a crucial role for communication between neurons [Izhikevich]. They are steep variations in the electric potential across a cell’s membrane, and they propagate in essentially constant shape from the soma (neuron’s body) along axons toward synaptic connections with other neurons. At the synapses they release an amount of neurotransmitter molecules depending upon the temporal sequences of spikes, thus transforming the electrical into a chemical carrier.

As a fact, neural communication is based on a temporal code whereby different cortical areas which have to contribute to the same percept P synchronize their spikes. Spike emission from a nonlinear threshold dynamical system results as a trade off between bottom-up stimuli to the higher cortical regions (arriving through the LGN (lateral geniculate nucleus) from the sensory detectors, video or audio) and threshold modulation due to top-down readjustment mediated by glial cells [Parpura and Haydon].

It is then plausible to hypothesize, as in ART (adaptive resonance theory [Grossberg1995a]) or other computational models of perception [Edelman and Tononi] that a stable cortical pattern is the result of a Darwinian competition among different percepts with different strength. The winning pattern must be confirmed by some matching procedures between bottom-up and top-down signals.

The neurodynamic aspect has been dealt with in a preliminary series of reports, that here I recapitulate as the following chain of linked facts.

1) A single spike in a 3D dynamics corresponds to a quasi-homoclinic trajectory around a saddle point (fixed point with 1 (2) stable direction and 2 (1) unstable ones); the trajectory leaves the saddle and returns to it (Fig.1).

2) A train of spikes corresponds to the sequential return to, and escape from, the saddle point. A control parameter can be set at a value B_C for which this return is erratic (chaotic interspike interval) even though there is a finite average frequency. As the control parameter is set above or below B_C, the system moves from excitable (single spike triggered by an input signal) to periodic (yielding a regular sequence of spikes without need for an input), with a frequency monotonically increasing with the separation DB from B_C (Fig.2)

3) Around the saddle point the dynamical system has a high susceptibility. This means that a tiny disturbance applied there provides a large response. Thus the homoclinic spike trains can be synchronized by a periodic sequence of small disturbances (Fig. 3). However each disturbance has to be applied for a minimal time, below which it is no longer effective; this means that the system is insensitive to broadband noise, which is a random collection of fast positive and negative signals.

4) The above considerations lay the floor for the use of mutual synchronization as the most convenient way to let different neurons respond coherently to the same stimulus, organizing as a space pattern. In the case of a single dynamical system, it can be fed back by its own delayed signal. As the delay is long enough the system is decorrelated with itself and this is equivalent to feeding an independent system. This process allows to store meaningful sequences of spikes as necessary for a long term memory [Arecchi et al.2001].

4- The role of synchronization in neural communications

The role of elementary feature detectors has been extensively studied in the past decades. Let us refer to the visual system [Hubel]; by now we know that some neurons are specialized in detecting exclusively vertical or horizontal bars, a specific luminance contrast, etc. However the problem arises: how elementary detectors contribute to a holistic (Gestalt) perception? A hint is provided by Fig.4 [Singer]. Both the woman and the cat are made of the same visual elements, horizontal and vertical contour bars, different degrees of luminance, etc. What are then the neural correlates of the identification of separate individual objects? We have one million fibers connecting the retina to the visual cortex, through the LGN. Each fiber results from the merging of approximately 100 retinal detectors (rods and cones) and as a result it has its own receptive field which is about 3.5 angular degrees wide. Each receptive field isolate a specific detail of an object (e.g. a vertical bar). We thus split an image into a mosaic of adjacent receptive fields, as indicated in the figure by white circles for the woman and black circles for the cat.

Now the “feature binding” hypothesis consists of assuming that all the neurons whose receptive fields are pointing to a specific object (either the woman or the cat) synchronize the spikes as shown in the right of the figure. Here each vertical bar, of duration 1 millisec, correspond to a single spike, and there are two distinct spike trains for the two objects.

Direct experimental evidence of this synchronization is obtained by insertion of microelectrodes in the cortical tissue of animals just sensing the single neuron [Singer]. Indirect evidence of synchronization has been reached for human beings as well, by processing the EEG (electro-encephalo-gram) data [Rodriguez et al.].

The advantage of such a temporal coding scheme, as compared to traditional rate based codes, which are sensitive to the average pulse rate over a time interval and which have been exploited in communication engineering, has been discussed in a recent paper [Softky].

Based on the neurodynamical facts reported above, we can understand how this occurs [Grossberg 1995a, Julesz]. In Fig.5 the central cloud represents the higher cortical stages where synchronization takes place. It has two inputs. One (bottom-up) comes from the sensory detectors via the early stages which classify elementary features. This single input is insufficient, because it would provide the same signal for e.g. horizontal bars belonging indifferently to the woman or to the cat. However, as we said already, each neuron is a nonlinear system passing close to a saddle point, and the application to a suitable perturbation can stretch or shrink the interval of time spent around, and thus lengthen or shorten the interspike interval. The perturbation consists of top-down signals corresponding to conjecture made by the semantic memory.

In other words, the perception process is not like the passive imprinting of a camera film, but it is an active process whereby the external stimuli are interpreted in terms of past memories. A focal attention mechanism assures that a matching is eventually reached. This matching consists of resonant or coherent behavior between bottom-up and top-down signals; that is why it has received the name ART as introduced by Grossberg (1976) and later specified in term of synchronization of the spike positions by Von der Malsburg has tested by Singer and his school. If matching does not occur, different memories are tried, until the matching is realized. In presence of a fully new image without memorized correlates, then the brain has to accept the fact that it is exposed to a new experience.

Notice the advantage of this time dependent use of neurons, which become available to be active in different perceptions at different times, as compared to the computer paradigm of fixed memory elements which store a specific object and are not available for others (the so called “grandmother neuron” hypothesis).

5- The self-organizing character of synchronized patterns

We have presented above qualitative reasons why the degree of synchronization represents the perceptual salience of an object. Synchronization of neurons located even far away from each other yields a space pattern on the sensory cortex, which can be as wide as a few millimeter-square, involving one million neurons. The winning pattern is determined by dynamic competition (the so-called “winner takes all” dynamics).

This model has an early formulation in ART and has been later substantiated by the synchronization mechanisms. Perceptual knowledge appears as a complex self-organizing process. We show how this approach overcomes earlier approaches of AI (Artificial Intelligence) and PDP (Parallel Distributed Processing) models.

Classical accounts of knowing and learning, influenced by the information processing paradigm, hold that procedural and declarative knowledge reside as information in long-term memory and are assembled during problem solving to produce appropriate solution The underlying assumption is that any cognitive agent possesses some language-like sign system to represent the world; cognition is said to occur when these sign systems are manipulated according to rules with IF….THEN…. structure [Anderson].

This classical approach to cognition, which posits some sign system as the necessary and sufficient condition for any cognitive agent to exhibit intelligence, is known as the physical symbol system hypothesis [Newell and Simon]. However, this approach, in which learning is conceived of as the rule-governed updating of a system of sentences encountered numerous failures to account for empirical data as [Churchland and Sejnowski]:

- the preanalytic human judgements of credibility which is the basis of any account of large scale conceptual change as the acceptance of a new scientific paradigm;

- the perceptual discriminations;

- the connections between conceptual and material practices which are the basis of manual activities;

- the speed with which human beings construct appropriate frames relevant to explanatory problems (the so-called “frame problem”).

In the PDP models the connectivity is realized by three layers consisting of input, hidden and output units (fig.6).

In contrast with the traditional computer models such networks are not programmed to contain procedural and declarative knowledge but are trained to do specific things [Churchland and Sejnowski]. The network is exposed to a large set of examples. Each time the output is compared to the “correct” answer, the difference is used to readjust the connection weights through the network. This is a form of training known as “back propagation”. However, a strong criticism [Grossberg 1995b] is that connections are fixed apriori and there is no self-organizing behavior as instead it occurs in the dynamical formation of a synchronized pattern.

A possible model for a patterned coupling of neurons across the sensorial cortex has been suggested by Calvin [Calvin] in analogy with the pattern formation at the top of a fluid layer heated from below. In both cases if the excitation range is fixed (in our case by the axon length), then the most likely configuration is an equilateral triangle, since each vertex confirms the other two. But each vertex can also be coupled to other equilateral triangles, yielding an overall mosaic pattern which looks as a floor of connected hexagons.

We have already discussed DSS (Arecchi et al.2002) and more generally we have studied (unpublished work) how a 1D or 2D lattice of homoclinic chaotic objects reaches a coherent synchronized configuration for small amounts of mutual coupling.

6- A metric in percept space

We discuss two proposals of metrics of spike trains. The first one [Victor and Purpura] considers each spike as very short, almost like a Dirac delta-function and each coincidence as an instantaneous event with no time uncertainty. The metric spans a large, yet discrete, space and it can be programmed on a standard computer.

A more recent proposal [Rossum] accounts for the physical fact that each spike is spread in time by filtering process, hence the overlap takes a time breadth t_c and any coincidence is a smooth process.

Discrete metrics

Victor and Purpura have introduced several families of metrics between spike trains as a tool to study the nature and precision of temporal coding. Each metric defines the distance between two spike trains as the minimal "cost" required to transform one spike train into the other via a sequence of allowed elementary steps, such as inserting or deleting a spike, shifting a spike in time, or changing an interspike interval length.

The geometries corresponding to these metrics are in general not Euclidean. Each metric, in essence, represents a candidate temporal code in which similar stimuli produce responses which are close and dissimilar stimuli produce responses which are more distant.

Spike trains are considered to be points in an abstract topological space. A spike train metric is a rule which assigns a non-negative number D(S_a,S_b) to pairs of spike trains S_a and S_b which expresses how dissimilar they are.

A metric D is essentially an abstract distance. By definition, metrics have the following properties:

· D(S_a,S_a)=0

· Symmetry: D(S_a,S_b)=D(S_b,S_a)

· Triangle inequality: D(S_a,S_c) £ D(S_a,S_b)+ D(S_b,S_c)

· Non-negativity: D(S_a,S_b)>0 unless S_a=S_b,

The metrics may be used in a variety of ways -- for example, one can construct a neural response space via multidimensional scaling of the pairwise distances, and one can assess coding characteristics via comparison of stimulus-dependent clustering across a range of metrics.

Cost-based metrics are constructed with the following ingredients:

· a list of allowed elementary steps (allowed transformations of spike trains)

· an assignment of non-negative costs to each elementary step

For any such set of choices one can define a metric D(S_a,S_a) as the least total cost of any allowed transformation from S_a to S_b via any sequence of spike trains S_a,S₁,S₂…,S_n,S_b.

Although this method has been applied successfully [MacLeod et al.], the calculation of the full cost function is quite involved. The reason is that it is not always clear where a displaced spike came from, and if the number of spikes in the trains is unequal, it can be difficult to determine which spike was inserted/deleted.

A continuous metric

Rossum has introduced an Euclidean distance measure that computes the dissimilarity between two spike trains . First of all, filter both spikes trains giving to each spike a duration t_c. To calculate the distance, evaluate the integrated squared difference of the two trains. The simplicity of the distance allows for an analytical treatment of simple cases.

The distance interpolates between, on the one hand, counting non-coincident spikes and, on the other hand, counting the squared difference in total spike count. In order to compare spike trains with different rates, total spike count can be used (large t_c). However, for spike trains with similar rates, the difference in total spike number is not useful and coincidence detection is sensitive to noise.

The distance uses a convolution with the exponential function. This has an interpretation in physiological terms.

Interestingly, the distance is related to stimulus reconstruction techniques, where convolving the spike train with the spike triggered average yields a first order reconstruction of the stimulus [Rieke et al.]. Here the exponential corresponds roughly to the spike triggered average and the filtered spike trains correspond to the stimulus. The distance thus approximately measures the difference in the reconstructed stimuli.

.

7- Role of duration T in perception: a quantum aspect

How does a synchronized pattern of neuronal action potentials become a relevant perception? This is an active area of investigation which may be split into many hierarchical levels. At the present level of knowledge, we think that not only the different receptive fields of the visual system, but also other sensory channels as auditory, olfactory, etc. integrate via feature binding into a holistic perception. Its meaning is “decided” in the PCF (pre frontal cortex) which is a kind of arrival station from the sensory areas and departure for signals going to the motor areas. On the basis of the perceived information, actions are started, including linguistic utterances.

Sticking to the neurodynamical level, and leaving to other sciences, from neurophysiology to psychophysics, the investigation of what goes on at higher levels of organization, we stress here a fundamental temporal limitation.

Taking into account that each spike lasts about 1 msec, that the minimal interspike separation is 3 msec, and that the average decision time at the PCF level is about T=240 msec, we can split T into 240/3 =80 bins of 3 msec duration, which are designated by 1 or 0 depending on whether they have a spike or not. Thus the total number of messages which can be transmitted is

2⁸⁰»10²⁷

that is, well beyond the information capacity of present computers. Even though this number is large, we are still within a finitistic realm. Provided we have time enough to ascertain which one of the 10²⁷ different messages we are dealing with, we can classify it with the accuracy of a digital processor, without residual error.

But suppose we expose the cognitive agent to fast changing scenes, for instance by presenting in sequence unrelated video frames with a time separation less than 240 msec. While small gradual changes induce the sense of motion as in movies, big differences imply completely different subsequent spike trains. Here any spike train gets interrupted after a duration DT less than the canonical T. This means that the PCF cannot decide among all perceptions coded by the neural systems and having the same structure up to DT, but different afterwards. How many are they: the remaining time is t=T-DT . To make a numerical example, take a time separation of the video frames DT=T/2, then t=T/2. Thus in spike space an interval DP comprising

2^t/3»2⁴⁰»10¹³

different perceptual patterns is uncertain.

As we increase DT, DP reduces, thus we have an uncertainty principle

DP^.DT³C

The problem faced thus far in the scientific literature, of an abstract comparison of two spike trains without accounting for the available time for such a comparison, is rather unrealistic. A finite available time DT places a crucial role in any decision, either if we are trying to identify an object within a fast sequence of different perceptions or if we are scanning trough memorized patterns in order to decide about an action.

As a result the perceptual space P per se is meaningless. What is relevant for cognition is the joint (P,T) space, since “in vivo” we have always to face a limited time DT which may truncate the whole spike sequence upon which a given perception has been coded. Only “in vitro” we allot to each perception all the time necessary to classify it.

A limited DT is not only due to the temporal crowding of sequential images, as reported clinically in behavioral disturbances in teenagers exposed to fast video games, but also to sequential conjectures that the semantic memory essays via different top-down signals. Thus, while the isolated localization of a percept P (however long is T) or of a time T (however spread is the perceptual interval DP) have a sense, a joint localization both in percept and time has an ultimate limit when the corresponding domain is less than the quantum area C.

Let us consider the following thought experiment. Take two percepts P1 e P2 which for long processing times appear as the two stable states of a bistable optical illusion, e.g the Necker cube. If we let only a limited observation time DT then the two uncertainty areas overlap. The contours drawn in Fig.7 have only a qualitative meaning. The situation is logically equivalent to the non commutative coordinate-momentum space of a single quantum particle.

Thus in neurophysics time occurs under two completely different meanings, that is, as the ordering parameter to classify the position of successive events and as the useful duration of a relevant spike sequence, that is, the duration of a synchronized train. In the second meaning, time T is a variable conjugate to perception P.

The quantum character has emerged for an interrupted spike train in a perceptual process. It follows that the (P,T) space cannot be partitioned into disjoint sets to which a Boolean yes/not relation is applicable and hence where ensembles obeying a classical probability can be considered. A set-theoretical partition is the condition to apply the Church-Turing thesis, which establishes the equivalence between recursive functions on a set and operations of a universal computer machine.

The quantum character of overlapping perceptions should rule out in principle a finitistic approach to perceptual processes. This is the negative answer to the Turing 1950 question whether the mental processes can be simulated by a universal computer [Turing].

Among other things, the characterization of the “concept” or “category” as the limit of a recursvive operation on a sequence of individual related perceptions gets rather shaky, since recursive relations imply a set structure. In perspective, also higher order linguistic tasks should be investigated by dynamical approaches as single elementary perceptions.

8 –Nonlinear dynamics and ontology

We have seen how feature binding provides a dynamical mean to perceive a whole individual with all its characteristics. Such a holistic approach is at variance with Galileo’s program which is the starting point of modern science. In his 1612 letter to M. Welser, Galileo says “not to attempt the essence (i.e. the nature),but limit oneself to quantitative affections, that is, single measurable appearances”. Let me refer to an example. If I speak of an apple without showing it, each interlocutor gets a different idea of the apple (green or red, large or small, etc). In order to have a general consensus, we give up speaking of the apple, split it into some relevant features that we can measure separately (flavor, color, shape, size etc) attribute a number to each feature, and model the apple as the collection of all these numbers. This was the starting point for the powerful link between mathematics and natural science; now the apple has been reduced to a N-ple of numbers, or geometrically to a point in an N-dimensional space. If we repeat the procedure for all objects of experience, then the mutual relations become mathematical relations within a set of numbers, that we can process by a formal language as that of a computer, extracting predictions. This way, we limit to descriptions and give away with explanations.

A logical problem arises: how many features are necessary to faithfully recover the apple? We face the limits of a set-theoretical language: the above question is undecidable in the Goedel sense.

Historically, the observed features have been reduced to the interplay of the elementary constituents (molecules, atoms etc). This was Newton’s approach, later extended to other interactions and now been pursued in view of a TOE (theory of everything). A breakthrough however was provided by introduction of nonlinear dynamics and the role of bifurcations, starting with Poincaré 1880. The collective dynamics of a large set of elementary bodies depends upon the setting of some, possibly a few, control parameters. Depending on such a setting the system may have different stable states, separated by bifurcations. In the last decades, the analysis of bifurcation has uncovered situations where nearby initial points in the appearance space lead to widely separated points after a time t: this has been called deterministic chaos. Among all bifurcations, Thom has focused his attention on the discontinuous ones which represent the boundaries of an object, defining its form in space (morphogenesis).

. Assume that we succeeded in describing the world as a finite set of N features, each one characterized by its own measured value being a real number, which in principle can take any value in the real domain (-¥,¥) even though boundary constraints might confine it to a finite segment L_i.

A complete description of a state of facts is given by the N- dimensional vector

(1)

The general evolution of the dynamical system is given by a set of N rate equations for all the first time derivatives . We summarize the evolution via the vector equation

(2)

where the function is an N-dimensional vector function depending upon the instantaneous values as well as on a set of external (control) parameters .

Solution of Eq. (2) with suitable initial conditions provides a trajectory which describes the time evolution of the system. We consider as ontologically relevant those features which are stable, that is, which persist in time even in presence of perturbations. To explore stability, we perturb each variable by a small quantity , and test whether the perturbation tends to disappear or to grow up catastrophically.

However complicated is the nonlinear function 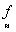, the linear perturbation of (2) provides for 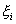simple exponential solutions versus time of the type

. (3)

The can be evaluated from the functional shape of Eq. (2). Each perturbation shrinks or grows in course of time depending on whether the corresponding stability exponent is positive or negative.

Now, as we adjust from outside one of the control parameters m , there may be a critical value

where one of the crosses zero (goes from + to -) whereas all the other remain positive. We call the exponent changing sign (u stays for “unstable mode”) and all the others (s stay for stable) (fig. 8 a).

Around , the perturbation tends to be long lived, which means that the variable has rather slow variations with respect to all the others, that we cluster into the subset which varies rapidly. Hence we can split the dynamics (2) into two subdynamics, one 1-dimensional (u) and the other (N-1) – dimensional (s), that is, rewrite Eq. (2) as

(4)

The second one being fast, the time derivative rapidly goes to zero, and we can consider the algebraic set of equations as a good physical approximation. The solution yields as a function of the slow variable

(5)

We say that the are “slaved” to . Replacing (5) into the first of (4) we have a closed equation for

(6)

First of all, a closed equation means a self consistent description, not depending upon the preliminary assignment of . This gives an ontological robustness to ; its slow dependence means that it represents a long lasting feature and its self consistent evolution law Eq. (6) means that we can forget about and speak of alone. For instance, in the case of the laser we are in presence of the onset of a coherent field ,which is the nature of the laser independently of details related to ( the laser can be due to atoms in gas or solids or free electrons in semiconductors and sizes ranging from 1 micrometer to several meters, but the are just appearances which DO NOT rule the laser nature). Such a holistic ,or emerging, feature provided by nonlinear dynamics was unknown to Galileo and Newton!

Furthermore as m crosses , a previous stable value is destabilized. A growing means that eventually the linear perturbation is no longer good, and the nonlinear system stabilizes at a new value (fig. 8 b).

Such is the case of the laser going from below to above threshold; such is the case of a thermodynamic equilibrium system going e.g. from gas to liquid or from disordered to ordered as the temperature at which it is set (here represented by ) is changed.

To summarize, we have isolated from the general dynamics (2) some critical points (bifurcations) where new salient features emerge. The local description is rather accessible, even though the general nonlinear dynamics f may be rather nasty.

Told in this way, the scientific program seems in line with perceptual facts, as compared to the shaky arguments of classical cognitivism. However it was based on a preliminary assumption, that there was a “natural” way of assigning the .

We have seen in Sec.2 that there are two avenues for assigning measurable parameters, that of Galileo, based on macroscopic features and that of Newton, based on the elementary components. Since the adiabatic elimination of the fast variables reduces the reliable (stable over long times and hence perceptually relevant) description to a few order parameters ,both avenues are equivalent even though Newton’s may appear more fundamental and Galileo’s less time consuming.

Once the problem has been formalized in some way, the amount of computational resources invested in the solution is called complexity (Arecchi,2000,2001) .The question however arises: is the formalization sufficient to extract the nature? In many man-made (artificial) situations(e.g. traffic, business, industrial or financial problems) the answer is YES. Instead, when we face natural phenomena ,from life to stars, we are in presence of open systems ,that we model with a given set of parameters without knowing if they are enough; in general they are NOT and the partial knowledge gives rise to different irreducible models (i.e. partial descriptions) which provide relevant information but only from a narrow point of view.

Fig 9 a) shows bifurcations implying discontinuous transitions; they are called catastrophes and represent the boundaries of confined objects ,thus they are associated with saliences (Thom).

Fig.9 b) shows multiple bifurcations. When many stable branches coexist we are in presence of many levels of reality ,each characterised by a different order parameter. We call description how a system behaves, that is , the dynamics of a single branch, and explanation the holistic interactions among the order parameters specifying the different branches. This second case does not require detailed knowledge of all but just the few .The interactions between two levels of reality represent a cause if one level is influencing the future asset of the other one and a purpose seen in the other direction. This way, we recover as global interactions philosophical categories with an ontological relevance, without having to atomize to the standard two body interactions of microscopic physics. They are by no means Kant’s apriori gadgets to relate observable entities. Indeed, the ontological statute of the levels of reality justifies the relevance of cause and purpose even if only one level of reality is under observation.

In conclusion, the refoundation of ontology based on nonlinear dynamics provides answers to old philosophical problems.

References

Allaria E., Arecchi F.T., Di Garbo A., Meucci R. 2001 “Synchronization of homoclinic chaos” Phys. Rev. Lett .86, 791.

Anderson J.R., 1985, “Cognitive Psychology and its Implications”, San Francisco, Ca :Freeman,

Arecchi F.T. 2000 “Complexity and adaptation: a strategy common to scientific modeling and perception” Cognitive Processing 1, 23.

Arecchi F.T. 2001, “Complexity versus complex system: a new approach to scientific discovery” Nonlin.Dynamics, Psychology, and Life Sciences, 5, 21.

Arecchi F.T., Meucci R., Allaria E., Di Garbo A., Tsimring L.S., 2002 “Delayed self-synchronization in homoclinic chaos” Pys.Rev.E65,046237

Brentano F. (1973), Psychology from an empirical standpoint, New York: Humanities Press (original 1874).

Calvin W.H. 1996 “The Cerebral Code: Thinking a Thought in the Mosaics of the Mind” Cambridge MA:MITPress

Churchland P.M. (1984), Matter and consciousness: a contemporary introduction to the philosophy of mind, Cambridge MA: M.I.T. Press.

Churchland P.S. and Sejnowski T.J., 1992, “The computational Brain”, Cambridge MA:MIT Press,

Dennett D. (1987), Intentional stance, Cambridge MA: MIT Press.

Edelman, G.M., and G. Tononi 1995 “Neural Darwinism: The brain as a selectional system” in “Nature's Imagination: The frontiers of scientific vision”, J. Cornwell, ed., pp.78-100, Oxford University Press, New York.

Fodor J.A. (1981), Representations, Philosophical essays on the foundations of cognitive science, Cambridge MA: MIT Press.

Grossberg S., 1995a “The attentive brain” The American Scientist, 83, 439.

Grossberg S., 1995b “Review of the book by F.Crick: The astonishing hypothesis: The scientific search for a soul” 83 (n.1)

Haken H. 1983 Synergetics, an introduction 3^rd edition,Berlin: Springer Verlag

Hubel D.H., 1995 “Eye, brain and vision”, Scientific American Library, n. 22, W.H. Freeman, New York.

Izhikevich E.M., 2000 “Neural Excitability, Spiking, and Bursting” Int. J. of Bifurcation and Chaos. 10, 1171

Julesz, B., 1991 “Early vision and focal attention”, Reviews of Modern Physics, 63, 735-772,

MacLeod, K., Backer, A. and Laurent, G. 1998. Who reads temporal information contained across synchronized and oscillatory spike trains?, Nature 395: 693–698

Meucci R., Di Garbo A., Allaria E., Arecchi F.T. 2002 “Autonomous Bursting in a Homoclinic System” Phys Rev.Lett. 88,144101

Newell A. and Simon H.A., 1976, “Computer science as empirical inquiry”, in J. Haugeland (Ed.), Mind Design (Cambridge: MIT Press), 35-66.

Parpura V. and Haydon P.G. 2000 “Physiological astrocytic calcium levels stimulate glutamate release to modulate adjacent neurons” Proc. Nat. Aca. Sci 97, 8629

Petitot J. (1990), Semiotics and cognitive sciences: the morphological turn, in The semiotic review of books, vol. 1, page 2.

Putnam H. (1988), Representation and reality, Cambridge MA: M.I.T. Press.

Pylyshyn Z.W. 1986 Computation and cognition, Cambridge MA: MIT Press

Quine W.V.O. (1969), Ontological relativity and other essays, New York: Columbia University Press.

Rieke, F., Warland, D., de Ruyter van Steveninck, R. and Bialek, W. 1996. “Spikes: Exploring the neural code”, MIT Press, Cambridge Mass..

Rodriguez E., George N., Lachaux J.P., Martinerie J., Renault B.and Varela F. 1999, “Perception's shadow:Long-distance synchronization in the human brain”, Nature 397:340-343.

Rossum van M. 2001 “A novel spike distance”, Neural Computation, 13, 751.

Singer W. E Gray C.M., 1995, “Visual feature integration and the temporal correlation hypothesis” Annu.Rev.Neurosci. 18, 555.

Thom R. (1983), Mathematical models of morphogenesis, Chichester: Ellis Horwood.

Thom R. (1988), Esquisse d’une semiophysique, Paris : InterEditions.

Turing A. 1950 “Computing Machinery and Intelligence” Mind 59, 433

Victor, J. D. and Purpura, K. P. (1997). “Metric-space analysis of spike trains: theory, algorithms and application” Network: Comput. Neural Syst. 8: 127–164.

Von der Malsburg C., 1981 “The correlation theory of brain function”, reprinted in E. Domani, J.L.

Van Hemmen and K. Schulten (Eds.), “Models of neural networks II”, Springer, Berlin.

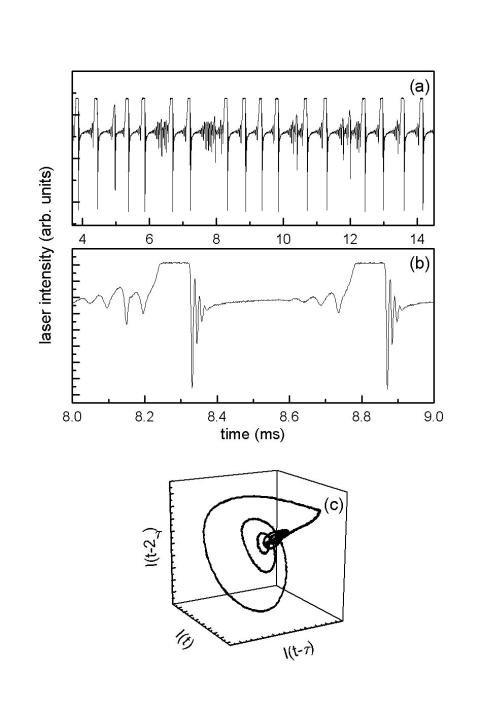
Fig. 1 : (a) Experimental time series of the laser intensity for a CO2 laser with feedback in the regime of homoclinic chaos. (b) Time expansion of a single orbit. (c) Phase space trajectory built by an embedding technique with appropriate delays [from Allaria et al.].

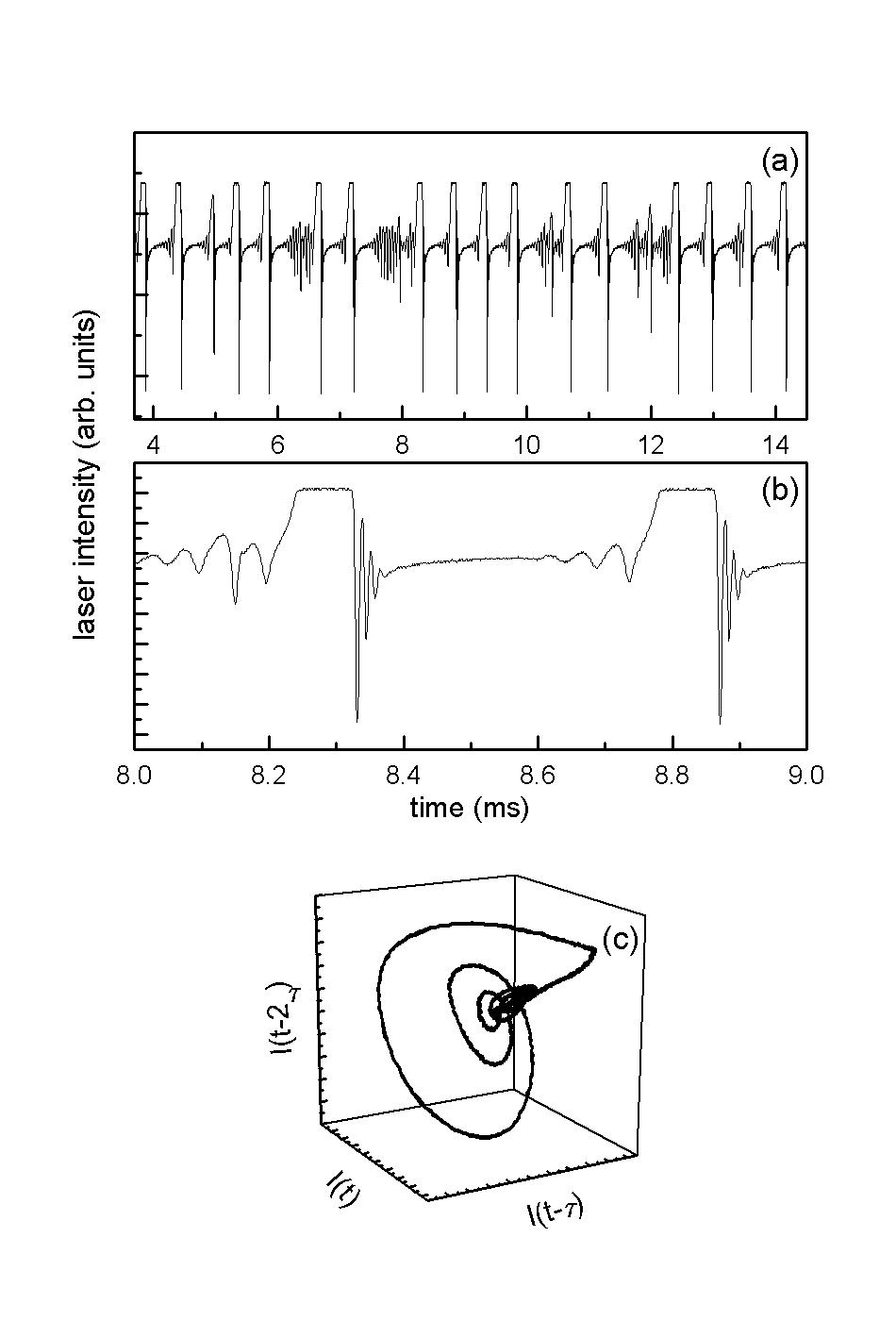
Fig.2 : Stepwise increase a) and decrease b) of control parameter B0 by +/- 1% brings the system from homoclinic to periodic or excitable behavior. c) In case a) the frequency n_r of the spikes increases monotonically with DB₀ [from Meucci et al.].

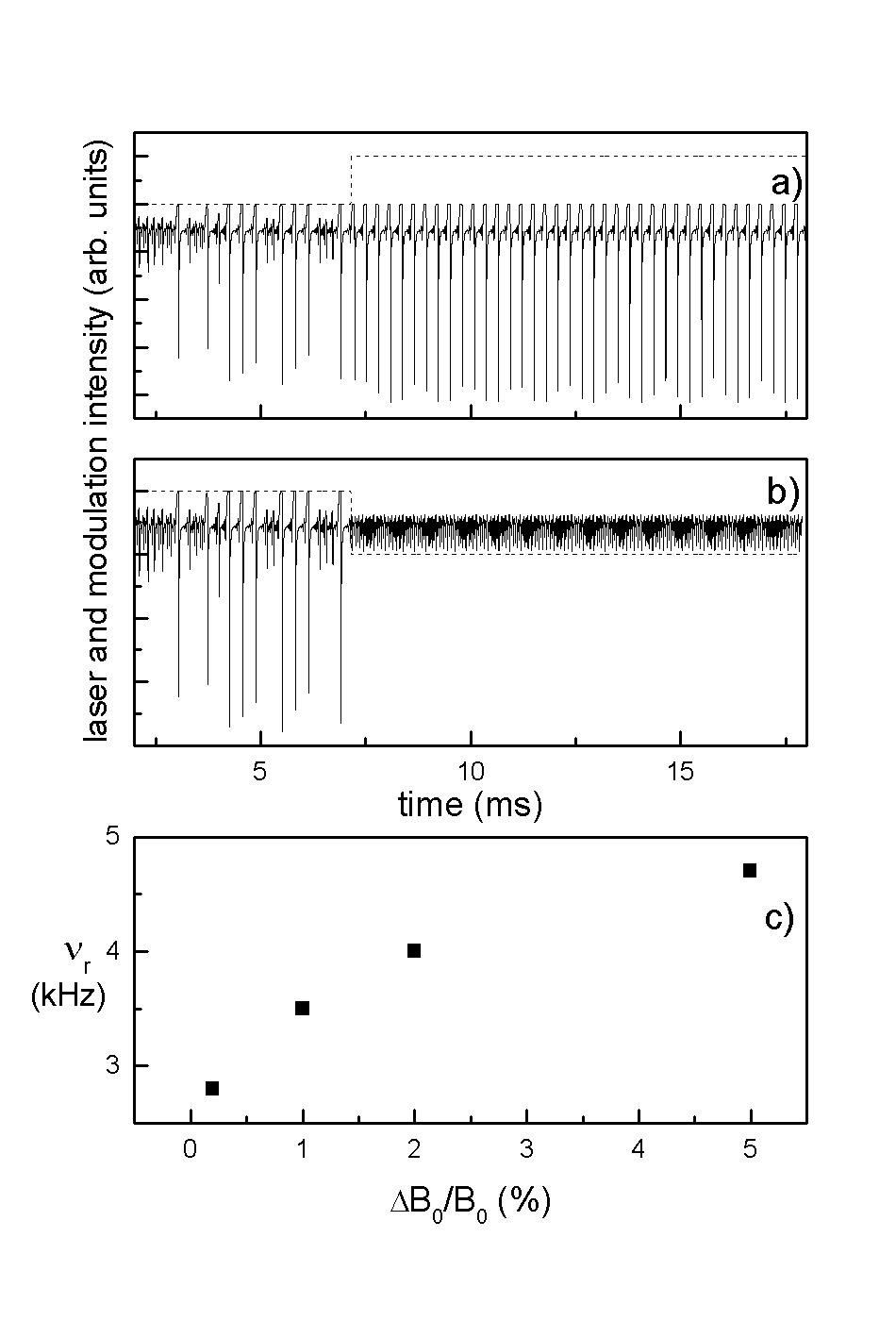
Fig. 3: Experimental time series for different synchronization induced by periodic changes of the control parameter. (a) 1:1 locking, (b) 1:2, (c) 1:3, (d) 2:1 [from Allaria et al.].

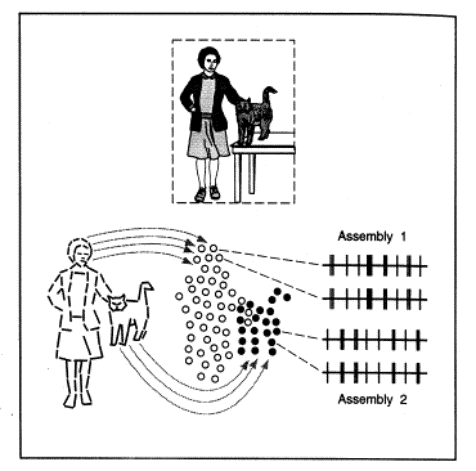
Fig. 4 : Feature binding: the lady and the cat are respectively represented by the mosaic of empty and filled circles, each one representing the receptive field of a neuron group in the visual cortex. Within each circle the processing refers to a specific detail (e.g. contour orientation). The relations between details are coded by the temporal correlation among neurons, as shown by the same sequences of electrical pulses for two filled circles or two empty circles. Neurons referring to the same individual (e.g. the cat) have synchronous discharges, whereas their spikes are uncorrelated with those referring to another individual (the lady) [from Singer].

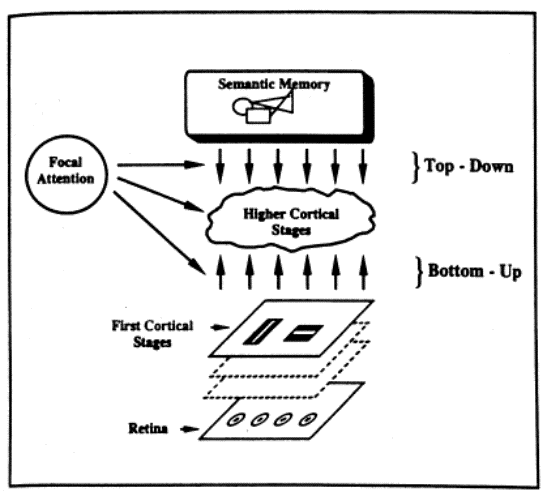
Fig.5 ART = Adaptive Resonance Theory. Role of bottom-up stimuli from the early visual stages an top-down signals due to expectations formulated by the semantic memory. The focal attention assures the matching (resonance) between the two streams [from Julesz].

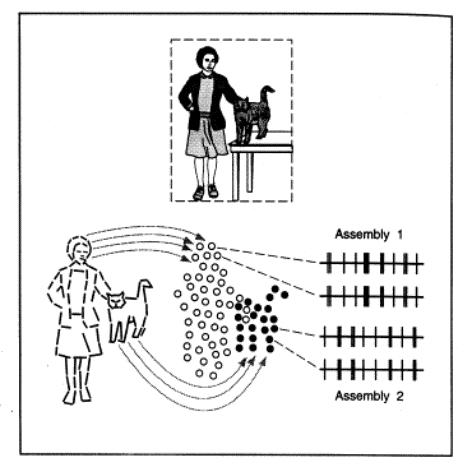
Fig.6 A simple network including one example of a neuronlike processing unit. The state of each neural unit is calculated as the sum of the weighted inputs from all neural units at a lower level that connect to it.

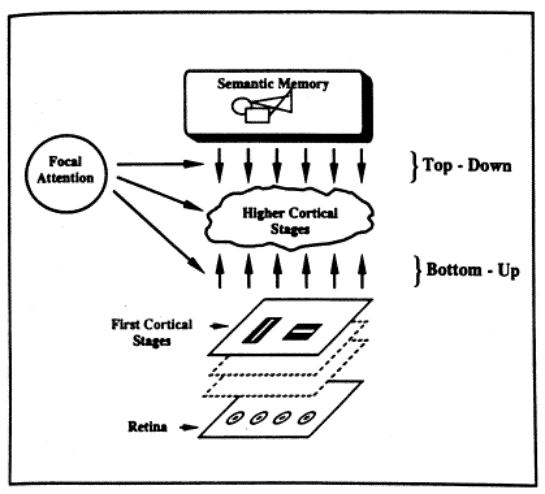
Fig.7 Uncertainty areas of two perceptions P₁ and P₂ for two different durations of the spike trains.

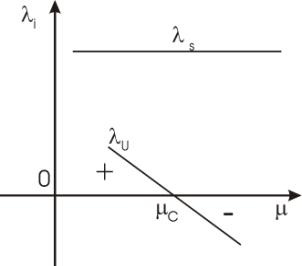
Fig. 8 a)As the control parameter m crosses the critical value m_c, the eigenvalues l_s remain positive, providing stable behavior to the corresponding dynamical variables x_s, whereas l_u goes from positive to negative, crossing zero where it destabilizes the corresponding parameter x_u, which then has a slow behavior (long autocorrelation)

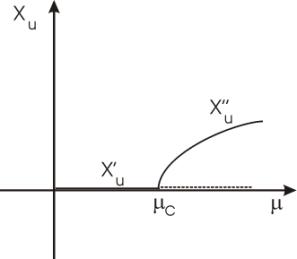
Fig. 8 b) Plot of the stationary solutions versus the control parameter: at m_c the branch x’_u becomes unstable (dashed branch) and a new stable branch x’’_u emerges from the bifurcation point.

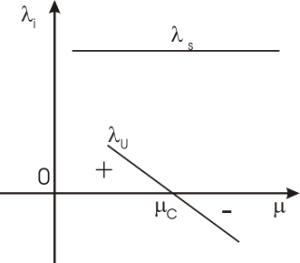
Fig. 9 a) direct and inverse pitchfork bifurcation: in the direct case the systems changes stable branch at m_c; in the inverse case, at m₁ and m₂ the stable branch is replaced by an unstable portion (dashed), as m is moved to right or left the system jumps discontinuously on the other branch and the bifurcation is called catastrophe (notice the hysteresis loop as m goes up and comes back)

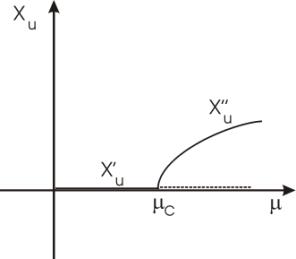
Fig. 9 b) Multiple bifurcation diagram. Solid (dashed) lines represent stable (unstable) steady states as the control parameter is changed.

---

* Presented at the International Colloquium on “Cognition,Meaning and Complexity. Self Organization in Cognitive Systems” Roma 14-15 June 2002