VI.
INDETERMINAZIONE E MISURAZIONE
Principi di limitazione
Abbiamo visto che in meccanica quantistica alla domanda sperimentale (A, D) non può corrispondere una proprietà, in quanto il PVP è messo seriamente in discussione dall’esempio di Kochen e Specker. Tuttavia le proprietà sono degli universali. Ad esempio, la proprietà “rosso” può essere applicata a diversi oggetti. Possiamo anche dire che il fatto che “per il sistema fisico S l’osservabile A ha valore compreso in D” non esiste. Dove intendiamo con fatto un universale. Esiste solo quello che possiamo chiamare l’evento che “per il sistema fisico S l’osservabile A ha valore compreso in D”. Dove la nozione di evento è strettamente individuale. Gli eventi quantistici possono essere individuati nello spazio e nel tempo, ma non essendo universali, non possono far parte a pieno titolo di alcuna rete teorica o esplicativa. Essi sono solo il risultato di una predizione o di una misurazione.
Dal teorema di Gleason possiamo dedurre il seguente principio di dispersione:
Non ci sono stati quantistici – puri o misti – che portano
la totalità degli eventi quantistici nell’insieme 
.
Nel caso di P (momento) e di Q (posizione):
Se per uno stato D, 
, allora 
per ogni intervallo G di
numeri reali e viceversa.
Il supporto di uno stato rispetto a un’osservabile data è l’insieme che contiene esattamente i valori di quella osservabile ai quali lo stato assegna probabilità non nulla.
Si può adesso formulare il principio del supporto:
Se A e B sono osservabili incompatibili, allora c’è uno stato puro D i cui supporti rispetto ad A e B non possono essere entrambi dei singoli eventi quantistici.
Nel caso di P e Q:
Se il supporto di D rispetto a Q è (Q, D), allora il supporto di D rispetto a P è l’intero ambito dei reali e viceversa.
Nel caso in cui gli operatori A e B delle osservabili incompatibili A e B non condividono autovettori, allora non vi è alcuno stato D i cui supporti rispetto ad A e B sono entrambi eventi singoli. La nozione di “evento singolo” andrebbe precisata. Il principio del supporto implica il principio di dispersione.
Abbiamo definito (12b) il valore di aspettazione di un’osservabile A che ha autovalori ai come una somma pesata del tipo:
Il valore di aspettazione dipende ovviamente dallo stato del sistema e viene misurato su un insieme di sistemi preparati alla stessa maniera.
E’ chiaro che, in generale, ogni singolo risultato di una misurazione differisce dal valore di aspettazione. Prendiamo il valor medio di questa differenza e facciamone il quadrato affinché sia sempre un numero positivo. La radice di tale numero è chiamata varianza o incertezza dell’osservabile A:
Siano A e B due operatori hermitiani sullo spazio di Hilbert H. Si definisce il loro commutatore come segue:
Il commutatore di A e B è 0 quando A e B commutano. Il commutatore è un operatore, anche se, in generale, non è hermitiano. Si può dimostrare che per tutte le coppie di osservabili A e B vale:
(25)
Cioè il prodotto delle incertezze di 2 osservabili è sempre maggiore della metà del valor medio del loro commutatore.
Possiamo ora formulare il principio di incertezza:
Esistono coppie di osservabili il cui commutatore è diverso da 0.
Si noti che tutte queste quantità dipendono dallo stato.
Si può facilmente calcolare il commutatore di P e Q:
Da cui, utilizzando la (25):
(26)
Che è la forma più nota del principio di incertezza per la posizione e il momento. Siccome P e Q sono operatori a spettro continuo la (26) non dipende dallo stato del sistema. Invece per osservabili incompatibili di cui almeno una ha autovettori una disuguaglianza del tipo della (26) non vale, perché il prodotto delle incertezze può essere reso arbitrariamente piccolo ponendo il sistema in un autovettore, in modo che l’incertezza di un’osservabile scende a 0. Questo non viola il principio di incertezza, che afferma solo che per alcuni stati il commutatore è diverso da 0.
Interpretazioni
La (26), che abbiamo dedotto dal formalismo della teoria, riguarda un insieme di sistemi preparati allo stesso modo. Nulla essa ci dice su quel che accade nel singolo sistema. Possiamo però interpretare DP e DQ come delle incertezze relative a un singolo sistema. Quindi anche la (26) si riferirà a un singolo sistema. Che la (26) valga per un singolo sistema lo chiamiamo principio di Heisenberg. Il principio di Heisenberg implica quello di incertezza per P e Q. Ora indaghiamo quali ragioni abbiamo a favore del principio di Heisenberg. Possiamo dividere il principio di Heisenberg in due parti:
1. è impossibile misurare su un sistema simultaneamente P e Q con accuratezza grande a piacere;
2. il limite inferiore del prodotto dell’inaccuratezza di P e Q misurate su un singolo sistema è dell’ordine della costante di Planck.
Di fatto non ci sono argomenti conclusivi a favore di 2. I classici esperimenti mentali proposti da Heisenberg dimostrano al massimo che misurando una delle 2 osservabili si disturba l’altra in modo inconoscibile di una quantità dell’ordine di grandezza di h, per cui non è possibile sapere il suo valore precedente alla misura. Inoltre nella letteratura più recente molti sostengono che questa soglia può essere abbassata.
Di fatto la teoria per quanto riguarda il singolo sistema impone solo il principio del supporto e non quello di incertezza, che riguarda invece insiemi di sistemi preparati allo stesso modo. Si noti inoltre, che quando almeno una delle 2 osservabili incompatibili ha autovalori non vi è nessuna ragione per cui debba esistere un limite inferiore del prodotto delle loro incertezze.
Veniamo ora agli argomenti a favore di 2. Prendendo le mosse dal formalismo, von Neumann (1932) ragiona nella maniera seguente nel caso delle osservabili a operatori con spettro discreto e non degenere.
i. Si assuma che la misurazione di un’osservabile A dia il risultato a. Allora una seconda misurazione della stessa osservabile eseguita subito dopo darà lo stesso risultato.
ii. Immediatamente prima della seconda misura la probabilità
che A valga a è 1. Quindi il sistema è nell’autovettore 
di A che
corrisponde all’autovalore a.
iii. La misura simultanea di A e B dovrebbe quindi lasciare il sistema in uno stato che fosse un autovettore sia di A sia di B.
iv. Se A e B sono incompatibili e non hanno autovettori in comune, allora 3. è impossibile. Se invece ne hanno, allora, se sono incompatibili, non possono averli tutti in comune. Quindi esisteranno valori di A e B che non potranno mai risultare simultaneamente.
Nel passo cruciale iv. l’argomento utilizza solo il principio del supporto e non quello di incertezza, che si riferisce a insiemi di sistemi.
Il passo i. è problematico, perché sono relativamente pochi i casi di misurazione che ammettono una seconda misurazione e alcuni sostengono che in certi casi tale seconda misurazione non darebbe lo stesso risultato. Pauli ha chiamato “misurazioni di prima specie” quelle che rispettano i. Dunque la dimostrazione di von Neumann vale solo per le misurazioni di prima specie. Ciò malgrado ci sono buone ragioni per ritenere che il punto 1. del principio di Heisenberg sia sostanzialmente corretto da un punto di vista teorico.
Si noti un’importante differenza concettuale fra il principio di incertezza e quello di Heisenberg. Se affianchiamo il PMF – cioè il principio della misura fedele - al punto 1. del principio di Heisenberg otteniamo il seguente enunciato:
Le osservabili P e Q di un singolo sistema non sono mai determinate simultaneamente con accuratezza grande a piacere.
Chiamiamo questo principio di indeterminazione. Per contro il principio di incertezza assieme al PMF non dà luogo al principio di indeterminazione, in quanto esso riguarda insiemi di sistemi. Ci possiamo chiedere allora se valga il principio di indeterminazione.
I celebri esperimenti concettuali di violazione del principio di Heisenberg nel passato parlerebbero contro il principio di indeterminazione.
1. Si consideri una particella preparata con momento
verticale
con errore sperimentale 
. La si mandi contro una parete su cui è praticata una
fenditura Dy
in modo che durante il tragitto non subisca interazioni.
2. Dopo il passaggio nella fenditura la particella viene diffratta e quindi il suo momento verticale cambia. A questo punto però conosciamo la posizione sull’asse delle y della particella nel momento in cui attraversa la fessura con precisione Dy e il suo momento verticale con precisione Dpy.
3. Non c’è nessuna ragione di principio che ci impedisce di diminuire i valori di Dy e Dpy quanto vogliamo, se non i limiti sperimentali. Quindi è possibile retrodire con precisione grande a piacere il valore simultaneo di P e Q.
L’esperimento proposto incontra però una difficoltà. Se vogliamo che la particella passi esattamente per la fessura Dy dobbiamo prepararla con posizione verticale con un errore pari a Dy. In quel momento però deve avere anche una precisione del momento pari a Dpy; per il principio di Heisenberg queste 2 quantità non possono essere diminuite a piacere. Si potrebbe ovviare a questa obiezione preparando un fascio di particelle con posizione verticale indeterminata, solo alcune delle quali passeranno la fenditura, per cui il precedente ragionamento varrebbe solo per quelle. A questo punto, però, siccome parliamo di insiemi di particelle, la violazione nel passato non sarebbe del principio di indeterminazione, ma di quello di incertezza. Il principio di incertezza, in un singolo caso, può essere violato, senza che venga messo in discussione.
Il problema della misurazione
Assumiamo che l’osservabile che vogliamo misurare sia A
rappresentata nello spazio di Hilbert HS del sistema S. Essa
può assumere 2 valori corrispondenti agli autovettori 
e 
. Lo strumento di misura M deve avere almeno 3 stati,
quello fondamentale 
e i 2 corrispondenti
a quelli del sistema 
; tutti ortogonali fra loro. Questi ultimi sono possibili
vettori di stato dello strumento nello spazio di Hilbert HM.
Rappresentiamo gli stati della coppia S+M nello spazio prodotto tensore HSÄHM.
Assumiamo che prima di effettuare la misura il sistema sia nello stato puro 
e l’apparato sia
nello stato fondamentale 
. Quindi lo stato di partenza di S+M è 
. S+M si evolve in accordo con l’equazione di
Schrödinger, per cui 
. Per la linearità di U, sarà:
(27)
Dove:
e 
sono gli stati puri del sistema S+M. Lo stato puro 
non è in generale
riducibile a stati puri di S e M, in quanto 
non è della forma 
. Infatti, come abbiamo visto nel paragrafo Sistemi
composti e il prodotto tensore, un vettore dello spazio HSÄHM, che non
sia esprimibile nella forma 
, in generale non è riducibile univocamente a 2 stati puri
rispettivamente di HS e HM. Esso sarà quindi rappresentabile
mediante 2 stati misti DS, e DM che sono
gli operatori densità che identificano lo stato rispettivamente di S e M.
Si può dimostrare che:
(28)
Ora, al fine di avere un risultato della misurazione,
dobbiamo interpretare DS, e DM come forme di ignoranza,
cioè come insiemi statistici di 2 stati puri pesati dai 2 coefficienti c1 e c2. Questo
però è impossibile, perché se S è nello stato 
o 
e M
corrispondentemente è nello stato 
o 
, allora S+M dovrebbe essere o nello stato 
o nello stato 
; e, invece, sappiamo che 
è una sovrapposizione
e non uno stato misto.
Arriviamo alla conclusione che, siccome l’equazione di Schrödinger porta stati puri in stati puri, essa non può rendere conto del passaggio da uno stato puro a uno stato misto interpretabile in termini di ignoranza, di cui ha bisogno il processo di misurazione.
Il postulato di proiezione
Consideriamo un sistema che si trovi in uno stato puro
descritto dal vettore 
. Esso per un’osservabile a spettro discreto e non degenere A
avrà probabilità pi che nella misurazione risulti l’autovalore ai. Ora, se
tale misura è di prima specie, allora lo stato del sistema dopo la misurazione
dovrà trovarsi nell’autostato di A 
. Dunque deve realizzarsi il seguente passaggio:
Questa richiesta introdotta da von Neumann, è stata chiamata da Margenau “postulato di proiezione”. Essa può essere formulata anche per le osservabili a spettro continuo nella seguente maniera.
Se la misurazione dell’osservabile A localizza il suo valore nell’intervallo di numeri reali D, allora il sistema che ne risulta deve avere supporto (A, D) per l’osservabile A.
In pratica, dopo la misurazione, lo stato del sistema deve essere tale che i numeri fuori da D abbiano tutti probabilità 0 di risultare in una nuova misura della stessa osservabile.
Il postulato di proiezione è applicabile in modo chiaro solo a quelle che abbiamo chiamato misurazioni del primo tipo. Esso comunque non fornisce alcuna spiegazione fisica di questo processo, per cui non può essere un’adeguata soluzione del problema della misurazione.
Possibili soluzioni
Un primo gruppo di soluzioni – che potremmo chiamare termodinamiche – si basa su un ragionamento del tipo seguente.
Esistono eventi quantistici per i quali le probabilità date
dallo stato puro (27) sono diverse da quelle date dallo stato misto (28).
Infatti consideriamo l’evento E a cui corrisponde il proiettore PE;
prendiamo solo l’operatore densità per l’apparato di misura DM. Allora
la probabilità che M sia nello stato P1 deve
essere uguale alla probabilità che M+S sia nello stato 
. Per la (18) sappiamo che:
Ricordando la definizione della traccia e scegliendo una
base ortonormale che contenga anche 
:
Sostituendo:
Ma:
Cioè è 1 quando i=j e 0 quando i¹j. Allora:
Invece, usando l’algoritmo statistico normale della meccanica quantistica:
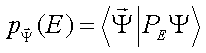
Sostituendo:
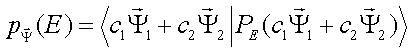
Sviluppando:
e 
Dove le 
rappresentano lo
stato di M e le 
di S.
