V. E’ POSSIBILE COMPLETARE LA MECCANICA QUANTISTICA?

Proprietà

In fisica classica le osservabili sono delle funzioni che associano dei numeri reali ai punti dello spazio degli stati in modo che a ogni questione sperimentale del tipo (A,D) in linea di principio si può rispondere con 1 o con 0, cioè essa è o vera o falsa. Questo significa che ontologicamente ha senso parlare di proprietà, intese come caratteristiche che un sistema possiede o non possiede, tertium non datur. Come abbiamo visto, in meccanica quantistica la situazione è assai diversa. Le osservabili in generale non permettono di attribuire i valori 0 o 1 a una questione sperimentale, ma solo una misura di probabilità compresa fra 0 e 1. Inoltre ci sono coppie di osservabili, come ad esempio le posizioni Q e i momenti P, tali che se a una domanda sperimentale che riguarda una delle 2 siamo in grado di rispondere con 1 o con 0, allora solo se D è l’intero ambito dei numeri reali è possibile rispondere con 0 o con 1 a una domanda sperimentale che riguarda l’altra osservabile.

Questa situazione potrebbe essere interpretata come una forma di ignoranza. Ovvero noi rappresentiamo il mondo fisico in questa maniera essenzialmente probabilistica, ma esso di fatto è perfettamente determinato, cioè se avessimo una maggiore conoscenza di come stanno le cose potremmo rispondere con 0 o 1 a tutte le domande sperimentali come accadeva in fisica classica. Se così stessero le cose il concetto di proprietà non avrebbe perso la sua rilevanza.

L’argomento di EPR

Formuliamo ora un tentativo di provare l’incompletezza della meccanica quantistica adombrata alla fine del paragrafo precedente. L’argomento è stato proposto originariamente (1935) da Einstein, Podolsky e Rosen (EPR) e modificato da Bohm (1951).

Consideriamo un sistema formato da un elettrone (e) e un positrone (p) e l’osservabile spin (S). Quest’ultima nel caso degli elettroni e dei positroni può assumere solo 2 valori e , che per semplicità chiameremo + e -. Essa può venir misurata lungo una qualsiasi direzione dello spazio, che indicheremo con le lettere greche a, b. Le osservabili spin lungo 2 direzioni diverse sono incompatibili. Lo stato di ognuna delle 2 particelle lo possiamo rappresentare in uno spazio H a 2 dimensioni. Per cui lo stato del sistema composto verrà rappresentato in uno spazio prodotto tensore H_eÄH_p. Siano e gli autovettori dell’osservabile spin misurato in una direzione a () sull’elettrone, e e gli autovettori dello spin misurato nella stessa direzione sul positrone (). Prepariamo il sistema in quello che viene chiamato stato di singoletto:

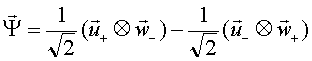(21)

Ricordando la (12), sappiamo che il sistema ha probabilità ½ di trovarsi nello stato + per l’elettrone e - per il positrone, e probabilità ½ di trovarsi nello stato - per l’elettrone e + per il positrone. E’ interessante il fatto che il vettore dello spazio H_eÄH_p è indipendente dalla direzione a in cui si decide di misurare lo spin, sempre che lo si misuri nella stessa direzione per i 2 sistemi. Consideriamo ora il caso in cui misuriamo nella direzione a sull’elettrone e nella direzione b sul positrone. La meccanica quantistica prevede che se il sistema composto è nello stato di singoletto (21), allora la probabilità che entrambe le misure diano + è data da:

(22)

Dove con ab indichiamo l’angolo fra le 2 direzioni. Se a e b coincidono la probabilità che entrambe le misure diano + è 0. Ovvero se sull’elettrone lo spin è + allora sul positrone è - o viceversa.

La probabilità di trovare + sull’elettrone e - sul positrone (o viceversa) misurando nella stessa direzione a è uguale a quella di trovare + su entrambi quando ab è uguale a 180°. Per cui:

(23)

Esaminate le caratteristiche dello stato di singoletto, introduciamo alcuni principi filosofici.

1. Condizione sufficiente affinché ci sia un elemento di realtà è che si possa prevedere con certezza senza disturbare il sistema una quantità fisica.

Si noti che:

a. La condizione è sufficiente e non necessaria.

b. Il criterio vale solo se non disturbiamo il sistema. Il concetto di disturbo non va inteso in relazione alla preparazione del sistema, ma alla misurazione. Ogni preparazione è in un certo senso un disturbo, ma non è di questo che qui si tratta.

c. Il criterio di realtà può anche essere formulato in termini probabilistici. Ma stiamo ora esaminando la possibilità di applicare il concetto classico di proprietà alla meccanica quantistica.

2. Una teoria si dice completa quando ogni elemento di realtà determinato dalla 1. ha una controparte teorica.

Si noti che;

a. Se non ci limitassimo agli elementi stabiliti dal criterio di realtà 1., allora a causa di una ragionevole non conclusività di ogni indagine del mondo fisico, ogni teoria sarebbe incompleta.

b. Controparte teorica significa che la quantità prevista con certezza deve essere rappresentabile matematicamente senza ambiguità.

3. Due sistemi si dicono separabili quando le loro proprietà possono essere determinate indipendentemente; si dicono invece locali quando non sussiste nessuna influenza istantanea fra i 2.

a. Ad esempio. prima dell’introduzione della relatività generale l’azione gravitazionale era considerata istantanea, per cui 2 qualsiasi masse classiche non potevano essere considerate locali. Per contro il campo magnetico e quello elettrico si trasmettono a velocità finita c.

b. In meccanica quantistica, non tutti i sistemi sono separabili, in quanto uno stato puro nello spazio prodotto tensore, come risulta dal punto 2 del paragrafo Sistemi composti e prodotto tensore, non ha un’unica scomposizione in stati puri dei sistemi componenti. Questo accade quando lo stato puro nello spazio prodotto tensore non è esprimibile nei termini del prodotto tensore di 2 vettori uno per ogni spazio. Come si può dimostrare questo è il caso dello stato di singoletto.

A questo punto possiamo formulare l’argomento. Lasciamo che le 2 particelle di una coppia elettrone-positrone in uno stato di singoletto si allontanino l’una dall’altra. Poi misuriamo l’osservabile sull’elettrone. Allora possiamo prevedere con certezza sulla base della (23) il valore dell’osservabile del positrone senza disturbarlo, se assumiamo che i 2 sistemi sono locali. Per cui, secondo il criterio di realtà, esiste un elemento di realtà che corrisponde a . Avremmo potuto però misurare lungo una direzione b diversa da a, prevedendo con certezza il valore di , e quindi esisterà un secondo elemento di realtà corrispondente a . D’altra parte e sono osservabili incompatibili, per cui, per la meccanica quantistica non possono essere entrambe determinate. Quindi la meccanica quantistica è incompleta.

Si noti che l’argomento si basa su quella che è stata chiamata la determinatezza controfattuale, in quanto solo la prima misura può essere effettivamente compiuta, per cui dobbiamo assumere che valga la seconda procedura senza realizzarla. E’ noto che le condizioni di verità dei controfattuali sono un complesso problema filosofico, per cui l’argomento può essere discusso anche sotto questo aspetto. Si può però formulare l’argomento senza ragionamenti controfattuali.

Prepariamo il sistema nello stato di singoletto dato dalla (21) al tempo t₀. Come nel caso precedente, al tempo t₁ misuriamo l’osservabile sull’elettrone. A partire dal risultato possiamo prevedere con certezza il valore di mediante la (22). Se vale la località, allora il valore dello spin del positrone non può essere stato prodotto dalla misura sull’elettrone. Questo significa che anche a un istante t’ precedente a t₁, ma successivo a t₀, lo spin del positrone era già determinato. All’istante t’ però la rappresentazione matematica del sistema composto è data ancora da (21), e quella del sottosistema positrone è una miscela dei 2 stati + e -, in quanto uno stato puro del tipo (21) non si riduce a 2 stati puri, ma a 2 miscele per i sottosistemi (si ricordi il punto 2. dell’ultimo paragrafo del cap. precedente). Quindi noi possiamo attribuire un elemento di realtà che non è rappresentato nella teoria.

Occorre anche sottolineare che la nozione di realtà non è essenziale all’argomento. Si può infatti anche ragionare nella maniera seguente. Se vale la località, è possibile prevedere con certezza il valore dello spin dell’altro sistema a cui la teoria, invece, attribuisce ancora un valore probabilistico.

Una semplice via d’uscita per evitare la conclusione sarebbe insita nell’utilizzo della nozione di separabilità. Si può infatti dire che i 2 sistemi elettrone e positrone, pur essendo locali, non sono separabili. Per cui non ha senso parlare delle proprietà dell’uno indipendentemente da quelle dell’altro. Tuttavia la non separabilità dei 2 sistemi nello stato di singoletto dipende dalla struttura matematica dello spazio prodotto tensore, non è quindi detto che sia una caratteristica effettiva della realtà fisica. Torneremo ancora su questo problema.

L’interpretazione statistica

Con interpretazione statistica della meccanica quantistica si intende l’idea che la descrizione dello stato tramite i vettori e gli operatori densità può essere applicata solo a insiemi di sistemi preparati alla stessa maniera e non a un singolo sistema. Tale interpretazione si basa su tre principi:

1. Principio del valore preciso PVP. In qualsiasi stato sia il sistema, ogni osservabile ha un preciso valore per il sistema individuale. Questo è il nucleo ontologico dell’interpretazione statistica. Questo valore preciso può essere, come è stato spesso chiamato, una variabile nascosta.

2. Principio della misura fedele PMF. Ogni misurazione rivela il valore di un’osservabile pre-esistente alla misura, relativa al sistema sotto osservazione. In base a questo principio, assieme al PVP, non solo ogni osservabile ha un valore preciso, ma esso è accessibile alla misura. Si noti che il PMF può valere anche se non vale il PVP. Infatti, nel caso in cui un’osservabile non abbia un valore preciso, ma solo un valore essenzialmente probabilistico, la misura potrà essere fedele nel senso che rispetta nei risultati tale probabilità.

3. Principio della frequenza relativa PFR. Gli algoritmi statistici della meccanica quantistica prevedono le frequenze relative dei valori delle osservabili su insiemi di sistemi preparati allo stesso modo. Per “frequenza relativa” si intende il numero dei casi favorevoli diviso il numero delle misurazioni effettuate. Ad esempio la (23) significa che su n misurazioni effettuate dello spin dell’elettrone e del positrone in circa dei casi risulterà lo spin dell’elettrone nello stato + e quello del positrone nello stato - , e in altri casi accadrà il contrario.

L’esempio di Kochen-Specker

Nel 1967 Kochen e Specker hanno fornito un argomento che mette seriamente in discussione il nucleo ontologico dell’interpretazione statistica.

Essi considerano un sistema di tripletto. Per un sistema a spin 1, l’osservabile spin in una direzione a può assumere 3 valori: +1, -1, 0. Allora, l’operatore , cioè il suo quadrato, può assumere solo i valori 1 e 0. Kochen e Specker hanno dimostrato che premesso che valga il PVP:

se a, b e g sono 3 direzioni ortogonali, allora dei 3 operatori 2 di essi devono avere valore 1 e il terzo 0.

Inoltre Kochen e Specker dimostrano che questa assegnazione non può essere fatta, contraddicendo il PVP.

Perché l’argomento funzioni occorre assumere che gli operatori rappresentino ognuno un’unica osservabile. Ovvero, il risultato di Kochen e Specker non sarebbe deducibile se ad esempio ammettessimo che l’operatore corrisponda a osservabili diverse in contesti di osservabili compatibili diversi. Ad esempio, possa avere valori diversi se fa parte della tripla o della tripla . Queste sarebbero osservabili non contestuali.

Generalizzazione

Assumiamo di avere un insieme pieno di osservabili (pieno nel senso che la scomposizione spettrale di queste osservabili deve comprendere tutti i raggi dello spazio H), ognuna delle quali ha n valori con , rappresentabili in uno spazio di Hilbert H. H avrà n dimensioni. A ogni ennupla di raggi corrisponderanno i valori a₁….a_n che può assumere un’osservabile A_i (assumiamo che non ci sia degenerazione). Questi raggi rappresentano le proprietà (A_i,a₁)……..(A_i,a_n).

Se vale il PVP allora di ogni ennupla di proprietà il sistema ne possiederà solo una. L’esempio di Kochen e Specker mostra che nello spazio di Hilbert a 3 dimensioni il PVP non vale. E’ possibile estendere questa conclusione a tutti gli spazi complessi con almeno 3 dimensioni.

In accordo con il PVP, assumiamo che esista una funzione f che porta tutti (è per questo che l’insieme delle osservabili deve essere pieno) i raggi dello spazio di Hilbert nell’insieme . Essa assegna 1 a un solo raggio di ogni ennupla che genera l’intero spazio. Tutte le premesse del teorema di Gleason sono soddisfatte, per cui esisterà un operatore densità D tale che per ogni raggio a:

D può essere scomposto come:

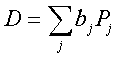
Possiamo trovare un insieme di raggi ortogonali fra loro che producono H, tali che ogni P_j di questa scomposizione proietta su uno dei membri di questo insieme. La funzione f rappresentata da D assumerà il valore 1 per un solo elemento di questo insieme, che chiamiamo i. Allora:

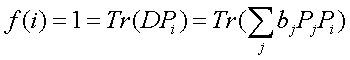
P_jP_i è =0 eccetto quando i=j. Inoltre ; per cui:

Perché la traccia di un proiettore su un raggio è =1. In quanto D è un operatore densità i coefficienti b_j sono tutti maggiori o uguali a 0 e la loro somma dà 1. Saranno dunque tutti 0 tranne b_i. Allora D è il proiettore P_i e per ogni raggio a dello spazio H diverso da i . Quindi:

Questo secondo la (18) è l’algoritmo statistico per gli stati puri.

Dove è un vettore normalizzato che giace nel raggio a. Siccome a non coincide con i, questa quantità è sempre minore di 1. Ne segue che la funzione f non può attribuire probabilità 1 ad altri raggi oltre a i. Il che contraddice l’ipotesi. Essa dunque non può esistere.

Si noti però che questa dimostrazione è stata condotta sulla base dell’assunzione che esista un insieme pieno di osservabili per lo spazio H. Non è detto che questo valga per la meccanica quantistica. Invece l’esempio di Kochen e Specker non utilizza questa premessa, in quanto è banalmente soddisfatta nel caso dello spin di un sistema in stato di tripletto, per cui è più incisivo nel mettere in discussione il PVP.

La disuguaglianza di Bell

Consideriamo una situazione di tipo EPR, composta da 2 sistemi che chiameremo 1 e 2, e misuriamo lo spin lungo 3 direzioni a, b e g. Se vale PVP e i 2 sistemi sono separabili possiamo attribuire un valore determinato a ognuna delle 6 osservabili . Tali valori sono o + o -; quindi le possibili combinazioni dei 6 risultati le possiamo indicare con una stringa di – e +. Le combinazioni sono 8, in quanto i valori devono essere anticorrelati, e ognuna avrà una certa probabilità di realizzarsi:

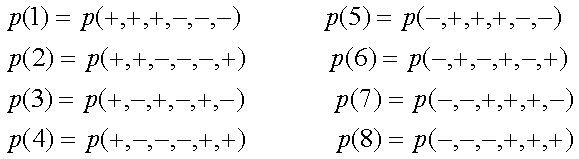
Facciamo ora l’ipotesi che i 2 sistemi siano locali, cioè che non ci sia fra essi influenza istantanea a distanza. Inoltre assumiamo PMF, cioè che i valori pre-esistenti delle osservabili siano fedelmente misurati. Allora possiamo dire che:

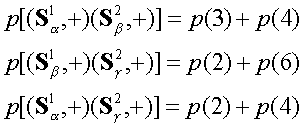
Tutte queste probabilità sono maggiori o uguali a 0, per cui:

(24)

Questa è la disuguaglianza proposta da Bell nel 1964, secondo la dimostrazione di Wigner (1970).

Utilizzando la (22) e assumendo PFR, cioè che le probabilità quantistiche siano delle frequenze relative su insiemi di sistemi preparati nello stesso modo, si possono calcolare i 2 termini previsti dalla meccanica quantistica e si vede che la (24) non viene sempre rispettata, ad esempio quando a,b e g sono complanari.

Si può anche dimostrare una disuguaglianza più generale, senza ipotizzare la perfetta anti correlazione data dalla (23), ma assumendo solo che i valori assoluti delle osservabili siano singolarmente presi minori o uguali a 1. Deve però valere che:

(24bis)

Cioè la probabilità congiunta dei risultati sui sistemi 1 e 2 deve essere uguale al prodotto delle probabilità, ovvero le due probabilità devono essere indipendenti. La (24bis) è anche chiamata “ipotesi di fattorizzabilità”. La nuova disuguaglianza, dimostrata da Clauser e Horn nel 1974 è anch’essa violata dalla meccanica quantistica ed è più facile da verificare sperimentalmente, poiché in pratica è molto difficile avere perfetta correlazione.

A questo punto abbiamo una sorta di esperimento cruciale. Da un lato abbiamo i 3 principi dell’interpretazione statistica più la località e la separabilità che implicano la disuguaglianza (24). Dall’altro la meccanica quantistica che la viola. Le probabilità che compaiono nella disuguaglianza di Clauser e Horne sono misurabili, per cui possiamo indagare il problema sperimentalmente. Gli esperimenti condotti finora, che sembrano decisivi, danno ragione alla meccanica quantistica. Quindi una delle premesse della disuguaglianza è errata. Sappiamo che il PVP per spazi con dimensione maggiore o uguale a 3 non vale. Però l’osservabile spin viene rappresentata in uno spazio a 2 dimensioni. D’altra parte 2 sistemi che interagiscono vengono rappresentati da un vettore nello spazio prodotto tensore, che ha 4 dimensioni. Quindi PVP non è detto che valga. D’altra parte, nello spazio prodotto tensore neanche la separabilità è detto che valga. Non possiamo invece eliminare la località, pena un conflitto con la relatività ristretta, che afferma che la velocità della luce è una velocità limite. Dunque la violazione sperimentale della disuguaglianza di Bell sembra imporci di abbandonare o PVP o la separabilità.

Notiamo che PVP non è essenziale alla dimostrazione, in quanto essa riguarda esclusivamente probabilità. Per la derivazione della disuguaglianza è sufficiente PMF, cioè che la misurazione sia fedele. Questo significa che la violazione sperimentale della disuguaglianza di Bell porta necessariamente alla negazione della separabilità. Resta da stabilire se la disuguaglianza di Bell sia dimostrabile sulla base della sola località senza la separabilità. Se così fosse dovremmo abbandonare anche la località.

La disuguaglianza di Bell non riguarda necessariamente situazioni quantistiche. Essa può essere dedotta per una qualsiasi coppia di sistemi distanti in cui un’osservabile dicotomica può essere misurata in almeno 3 modi diversi. Il fatto che essa sia effettivamente violata da coppie di sistemi quantistici ci informa che la rappresentazione delle interazioni fra sistemi fisici nello spazio prodotto tensore, che è caratterizzata da un’intrinseca non-separabilità dovuta alla maggior ricchezza di questo spazio rispetto ai singoli spazi, è necessaria. Alla fine del paragrafo sull’EPR avevamo osservato che l’argomento a favore dell’incompletezza della meccanica quantistica non poteva essere disinnescato utilizzando la nozione di non-separabilità, in quanto essa era più una caratteristica della matematica che dei sistemi fisici. Adesso sappiamo che la non-separabilità ha un fondamento fisico, almeno all’interno della rappresentazione quantistica del mondo.

Sicuramente la non-località è in contrasto con la relatività ristretta; resta aperto il problema se anche la non-separabilità sia in contrasto con la relatività. In prima approssimazione si può dire che essa non consente di mandare dei segnali superluminali, però la rappresentazione dello stato come non-separabile è profondamente diversa da quella della relatività.