III. LE CAPACITA’ RAPPRESENTATIVE DELLO SPAZIO DI HILBERT

Il principio di sovrapposizione

Cerchiamo ora di comprendere cosa significa rappresentare un sistema fisico nello spazio di Hilbert. Facciamo l’ipotesi che il sistema abbia una sola osservabile e sia determinato, cioè che a ogni possibile risultato di una misurazione sia associabile o probabilità 0 o probabilità 1. Questo significherebbe che ogni vettore di stato giacerebbe all’interno di uno dei possibili sottospazi individuati dagli autovettori dell’osservabile. In altre parole, se indichiamo con lo stato e con P_i i proiettori nei sottospazi degli autovalori dell’osservabile, avremo che ci sarà un solo valore i per cui:

In base alla (9) l’espressione sulla sinistra fornisce la probabilità che lo stato dia l’iesimo risultato. Mentre per tutti gli altri P_j diversi da i:

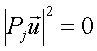
In meccanica quantistica, però, vale il principio di sovrapposizione, che afferma:

Se e rappresentano stati possibili del sistema, allora anche il vettore , ammesso che sia normalizzato, rappresenterà uno stato possibile del sistema.

E’ possibile mostrare che se i sistemi fisici vengono rappresentati nello spazio di Hilbert e vale il principio di sovrapposizione, non è possibile che tutti i risultati possibili di una misura siano determinati. Infatti in una situazione determinata sono possibili solo vettori di stato che giacciono nei sottospazi individuati dagli autovettori dell’osservabile, mentre, se vale il principio di sovrapposizione, sono possibili anche vettori che sono una combinazione lineare dei suddetti. Tali combinazioni lineari in generale non giacciono in un sottospazio corrispondente a un autovettore. E quindi la situazione non potrà essere determinata.

Stati puri e stati misti

Un vettore di stato che fornisce le informazioni sulla probabilità dei possibili risultati di un osservabile viene chiamato uno stato puro, nel senso che queste probabilità pertengono a ogni singolo sistema che viene preparato in quello stato, anche se il controllo sperimentale di quelle probabilità non può che essere effettuato su un insieme di sistemi preparati alla stessa maniera.

In contrapposizione al concetto di stato puro abbiamo quello di stato misto. Uno stato misto rappresenta una statistica su un insieme di possibili stati puri. Esso non è uno stato puro, quindi non può essere rappresentato come una combinazione lineare di stati puri, che, per il principio di sovrapposizione, sarebbe a sua volta uno stato puro. Per rappresentare uno stato misto dobbiamo perciò utilizzare gli operatori che proiettano sui raggi individuati dagli stati puri su cui facciamo la statistica. Allora, se sono possibili stati puri e P₁,P₂… sono i rispettivi proiettori e b₁,b₂… sono le probabilità che il sistema si trovi rispettivamente negli stati , allora uno stato misto è dato da:

In generale questa somma non è un operatore di proiezione, per cui essa non è rappresentabile da uno stato puro. In prima approssimazione possiamo dire che le probabilità implicite in uno stato puro sono inerenti allo stato fisico, mentre quelle presenti in uno stato misto sono dovute alla nostra ignoranza, cioè al fatto che non sappiamo in quale stato puro il sistema si trovi.

Osservabili e operatori

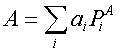
Consideriamo un’osservabile A che può assumere i valori a₁,a₂…..Ci chiediamo perché è ragionevole rappresentarla mediante un operatore hermitiano. Prendiamo un operatore hermitiano che abbia come autovalori a₁,a₂…..Esso dividerà lo spazio in sottospazi su cui proiettano gli operatori Per il teorema di scomposizione spettrale sappiamo che:

Supponiamo inoltre che lo spettro di A sia discreto, finito e non degenere, allora tale scomposizione è unica (a certe condizioni l’unicità vale anche nel caso infinito). Gli operatori hermitiani sono in un certo senso delle distribuzioni di possibili valori dell’osservabile. Inoltre a ogni proiettore è associata una probabilità data dall’algoritmo (9).

Compatibilità

Prendiamo le mosse dalla seguente definizione:

In ogni spazio vettoriale V i sottospazi L_a e L_b sono compatibili se esistono sottospazi di V tra loro ortogonali tali che

Col simbolo Å indichiamo la somma fra spazi, che possiamo intendere come una generalizzazione della somma fra 2 vettori.

In pratica 2 sottospazi sono compatibili se hanno in comune un sottospazio che è ortogonale a ciò che deve essergli aggiunto per formare i 2 spazi. Ad esempio nello spazio reale a 3 dimensioni il piano perpendicolare all’asse z e il piano perpendicolare all’asse y sono compatibili, perché hanno in comune l’asse delle x che è ortogonale, rispettivamente all’asse delle y e delle z, unito con le quali dà i suddetti piani.

Si può dimostrare che 2 sottospazi sono compatibili esattamente quando i rispettivi proiettori commutano.

Diamo allora la seguente definizione:

2 osservabili sono compatibili quando la loro rappresentazione mediante autovettori produce lo stesso spazio vettoriale e in questa rappresentazione ogni coppia di sottospazi legati ai possibili risultati è compatibile.

Se rappresentiamo gli operatori corrispondenti a 2 osservabili A e B mediante il teorema di scomposizione spettrale:

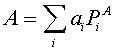
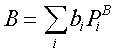
vediamo che se A e B sono compatibili allora gli operatori e commutano fra loro. Per cui se 2 osservabili sono compatibili allora i corrispondenti operatori commutano fra loro.

Consideriamo un’osservabile A con soli 2 autovalori a₁ e a₂. Ognuno dei 2 autovalori avrà rispettivamente probabilità c₁ e c₂ di risultare nella misurazione con c₁+c₂=1. Per la (12) possiamo rappresentare questo con un vettore in uno spazio a 2 dimensioni dove e sono i rispettivi autovettori. Prendiamo un’altra osservabile B con soli 2 autovalori b₁ e b₂ e probabilità normalizzate g₁ e g₂. Analogamente al caso precedente possiamo rappresentare questa situazione con un vettore . Dati i valori dei 4 coefficienti c₁,c₂,g₁,g₂ è possibile trovare una rotazione di tale che esso si sovrapponga esattamente a . In generale, però, tale rotazione non produce la sovrapposizione per valori diversi di c₁,c₂,g₁,g₂.

Diamo allora la seguente definizione:

2 osservabili sono mutuamente trasformabili se sono rappresentabili in un unico spazio di Hilbert H da 2 operatori A e B ed esiste un operatore unitario U in H tale che A=UBU^-1.

L’ultima equazioni dice che: applicare l’operatore A a un vettore è come applicare prima la rotazione U, poi applicare B e poi la rotazione inversa U^-1. In pratica, se 2 osservabili sono mutuamente trasformabili è sempre possibile rappresentare i loro risultati con lo stesso vettore di stato. Infatti, se, ad esempio, scegliamo il vettore di stato espresso mediante gli autovettori di B, per rappresentare A è sempre sufficiente applicare la rotazione U al vettore prescelto.

La caratteristica interessante dei sistemi quantistici, che li rende particolarmente adatti a essere rappresentati nello spazio di Hilbert, è che essi hanno parecchie coppie di osservabili incompatibili, ma spesso queste coppie sono anche di osservabili mutuamente trasformabili. Questo, ad esempio, vale per la più celebre fra le coppie di osservabili incompatibili, cioè posizione e momento. Che quindi, pur essendo incompatibili, possono essere rappresentate dallo stesso vettore di stato.

Principio di sovrapposizione e principio di indeterminazione

Torneremo sul principio di indeterminazione; per adesso lo possiamo enunciare approssimativamente come l’affermazione che esistono osservabili incompatibili. Il principio di sovrapposizione dice quali stati sono ammissibili, mentre quello di indeterminazione quali combinazioni di osservabili possono essere determinate. Come abbiamo già visto, il principio di sovrapposizione è sufficiente a rendere la rappresentazione di un sistema fisico nello spazio di Hilbert essenzialmente probabilistica. Lo stesso vale per il principio di indeterminazione. Infatti, se ci sono 2 osservabili incompatibili A e B, allora ci saranno 2 sottospazi incompatibili corrispondenti rispettivamente ai risultati x_i di Ae y_i di B. Ne segue che, se p(x_i)=1 allora . Ovvero in alcuni casi, se il valore di un’osservabile è determinato, quello dell’altra è essenzialmente probabilistico.

Sebbene entrambi i principi abbiano come conseguenza che la teoria sia essenzialmente probabilistica, essi sono concettualmente indipendenti. Inoltre, si può dimostrare che se valesse solo il principio di sovrapposizione, cioè non ci fossero osservabili incompatibili, allora non sarebbe possibile distinguere fra uno stato puro e uno stato misto, cioè tutte le probabilità potrebbero essere interpretate come una sorta di ignoranza. Questo significa che i due principi sono epistemologicamente connessi.