II.
STATI E OSSERVABILI
Lo stato classico
Consideriamo un sistema classico composto da N
particelle. Ognuna avrà una posizione nello spazio individuata da 3 coordinate
(qx,
qy,
qz)
e uno stato di moto individuato dal momento (velocità per massa) nelle 3
direzioni (px, py, pz). Le posizioni e i momenti sono in generale
sufficienti a identificare lo stato di un sistema classico. Lo stato del
sistema è quindi determinato in ogni istante da 6N variabili. Possiamo
allora rappresentarlo a un dato istante con un punto in uno spazio a 6N
dimensioni; su ogni dimensione proiettiamo il valore che assume la variabile
corrispondente. Questo spazio si chiama spazio delle fasi (F).
Ogni variabile A può essere considerata come una funzione che va dal
punto dello spazio delle fasi che rappresenta lo stato all’insieme dei numeri
reali, 
.
Se conosciamo il punto istantaneo St che rappresenta lo stato del sistema, possiamo porci la domanda sperimentale: la variabile A del sistema all’istante t ha un valore che cade nell’intervallo di numeri reali D? Tale domanda può avere solo 2 risposte, affermativa o negativa. Possiamo allora considerare la domanda come una funzione w che assegna alla variabile A e all’intervallo D lo 0 se la risposta è negativa e l’1 se la risposta è positiva. Possiamo allora dire che:
se e solo se 
Si noti che in fisica classica lo stato e l’insieme delle variabili sono esattamente la stessa cosa, come è abbastanza ovvio aspettarsi. Inoltre il valore della funzione w è determinato univocamente dalla funzione fA. Questo non vale invece in meccanica quantistica.
Lo stato quantistico
Lo stato quantistico non può essere rappresentato nello
spazio delle fasi. Esso ha invece bisogno di tutta la potenza rappresentativa
dello spazio di Hilbert. Lo stato quantistico è infatti rappresentabile come un
vettore nello spazio di Hilbert. La differenza fondamentale con il caso
classico è che le variabili – che in meccanica quantistica vengono chiamate
inopportunamente[1] osservabili
– non sono delle funzioni a variabile reale, ma degli operatori hermitiani.
Quando questi operatori hanno autovalori, allora essi rappresentano i possibili
valori che può assumere l’osservabile. Poniamo il caso che vogliamo misurare
l’osservabile A. Se il vettore corrispondente allo stato del sistema
giace su un raggio individuato da un autovettore dell’operatore corrispondente A,
allora la probabilità che il risultato della misurazione sia l’autovalore
corrispondente è 1. Se, invece, come accade nella maggior parte dei casi, il
vettore di stato non giace su un raggio individuato da un autovettore di A,
allora solo la probabilità che l’osservabile assuma l’autovalore corrispondente
è determinata. Poniamo che l’autovettore sia 
a cui corrisponde
l’autovalore ai e chiamiamo 
l’operatore che
proietta nel raggio che contiene 
. Allora, secondo la meccanica quantistica, la probabilità 
che una misurazione
dell’osservabile A su un sistema nello stato 
dia come risultato ai è data da:
(9)
La seconda uguaglianza è una conseguenza di (5). Se 
è normalizzato,
allora, sempre per la (5), il valore di tale probabilità varierà fra 0 e 1,
come deve essere. In pratica, la probabilità che l’osservabile A abbia
il valore ai è data dal prodotto scalare fra il vettore di stato
e la sua proiezione sul raggio individuato dall’autovettore 
corrispondente.
Indichiamo con 
lo spazio – che è
unidimensionale se A non ha autovalori degeneri – che contiene
l’autovettore 
dell’operatore A,
ovvero il sottospazio su cui proietta 
. Allora se lo stato appartiene a 
:
Cioè la probabilità che l’osservabile A abbia valore ai è 1, che equivale alla certezza.
Consideriamo ora il caso in cui l’osservabile A non
ha autovalori, ma è a spettro continuo, come, ad esempio, per la posizione.
Allora a ogni intervallo D sulla linea dei numeri reali corrisponde un sottospazio
tale che una misura
di A dà un valore all’interno di D con certezza se e solo se
lo stato 
del sistema
appartiene a 
. Questa è una generalizzazione del caso precedente. Se 
è il proiettore su 
, allora:
(10)
Questo vale sia per gli operatori a spettro continuo, sia per quelli a spettro discreto. Si noti che gli operatori di proiezione sono quelli che compaiono nel teorema di scomposizione spettrale. Questa formula collega le probabilità dei risultati sperimentali con le loro previsioni teoriche.
A una domanda sperimentale quantistica corrisponde
allora un operatore di proiezione 
o, che è lo stesso,
il sottospazio 
su cui esso proietta.
Perciò vediamo che in generale in meccanica quantistica le risposte alle
domande sperimentali hanno carattere probabilistico. Inoltre lo stato non è
definito dalle variabili, ma serve a calcolarle mediante l’algoritmo statistico
dato dalla (10).
Probabilità e valori di aspettazione
Se l’osservabile ha un operatore a spettro discreto i cui
autovalori non sono degeneri e 
sono i suoi
autovettori normalizzati, allora 
è una base ortonormale
dell’intero spazio e quindi esiste per ogni vettore di stato 
un solo insieme di
numeri complessi c1, c2……. tali che:
(11)
Se 
è normalizzato, vale
anche:
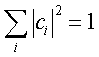
Si può allora dimostrare che le probabilità quantistiche date dalla (9) assumono una forma molto semplice:
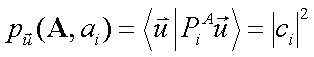(12)
In altre parole, la probabilità è data dal modulo quadrato del coefficiente dell’autovettore corrispondente nella scomposizione (11) del vettore di stato.
Può essere utile calcolarsi il valore medio che si ottiene
per un’osservabile misurata su un grande numero di sistemi preparati allo
stesso modo, chiamato anche valore d’aspettazione. Il valore d’aspettazione
di un’osservabile A
è ottenuto pesando ogni possibile risultato mediante la sua
probabilità:
(12b)
Utilizzando il teorema di scomposizione spettrale si ottiene:
(13)
Ovvero il valore di aspettazione di un’osservabile è dato dal prodotto scalare fra il vettore di stato e il vettore di stato trasformato dal corrispondente operatore. Questo vale sia per gli operatori a spettro continuo, sia per quelli a spettro discreto.
L’evoluzione dello stato in meccanica classica
Consideriamo una quantità fisica x che varia nel tempo. Essa può essere descritta da una funzione x=f(t). Prendiamo questa funzione negli istanti successivi t1 e t2. Possiamo così esprimere il tasso di variazione della quantità x nel periodo fra t1 e t2:
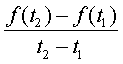
Ora vogliamo misurare il tasso di variazione di x esattamente nell’istante t. Allora consideriamo un intervallo temporale piccolissimo Dt e calcoliamo:
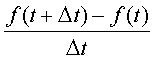
che è analoga alla precedente. Passiamo al limite, cioè facciamo tendere a 0 l’intervallo di tempo e avremo esattamente il tasso di variazione della variabile x all’istante t, chiamato anche derivata di x rispetto al tempo e indicato nella maniera seguente:
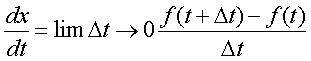
Il concetto fu introdotto da Newton, proprio per calcolare
la velocità istantanea di un corpo, ma la notazione che utilizziamo è più
simile a quella inventata da Leibniz negli stessi anni. Si noti che non tutte
le funzioni sono derivabili; in via approssimata si può dire che una funzione è
derivabile quando non si comporta in maniera “cattiva”. Ad esempio, la funzione
non è derivabile
rispetto a t quando t=0, poiché il suo valore va all’infinito.
Possiamo avere il caso di una funzione che dipende da più variabili. Ad esempio y=f(x,t). Possiamo allora definire la cosiddetta derivata parziale, che fornisce il tasso di variazione della quantità y solo rispetto a una variabile, che si indica così:
In meccanica classica possiamo esprimere la dinamica del sistema nei termini della sua energia totale o hamiltoniana, senza utilizzare più il concetto di forza. Come abbiamo già visto, lo stato di un sistema è definito dalle p e dalle q, cioè dai momenti e dalle posizioni. L’hamiltoniana (H) può essere espressa in funzione delle p e q. Se indichiamo con la derivata rispetto al tempo la variazione di una variabile, le equazioni di Hamilton-Jacobi permettono di calcolare le variazioni rispetto al tempo delle p e delle q:
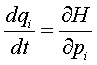e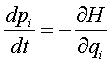 
La funzione H deve essere continua e derivabile. Queste sono 2i equazioni differenziali, che se risolte, forniscono la dipendenza delle variabili q e p rispetto al tempo. Si noti che le equazioni di Hamilton-Jacobi determinano i valori delle p e delle q in ogni istante, per cui si può dire che la meccanica classica in linea di principio è deterministica.
L’evoluzione dello stato in meccanica quantistica
Anche in meccanica quantistica l’evoluzione dello stato può essere espressa mediante l’hamiltoniana, che però non è più una funzione a variabile reale, ma un operatore hermitiano. L’equazione che esprime la variazione dello stato del sistema rispetto al tempo è la seguente:
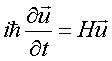(14)
Questa si chiama equazione di Schrödinger. In altre
parole, la variazione del vettore di stato 
è data
dall’applicazione al medesimo dell’operatore hamiltoniano.
Sulla base dell’hamiltoniana possiamo costruire un operatore Ut che, applicato allo stato presente fornisce lo stato in un qualsiasi altro istante t. Con ovvia notazione avremo allora:
Ut si può calcolare a partire dall’hamiltoniana nella maniera seguente:
(15)
Dove l’espressione sulla destra è uguale alla somma infinita di operatori:
Ut è un operatore unitario, cioè esso, se
applicato a un vettore, conserva la lunghezza di quest’ultimo ed per 2
qualsiasi vettori 
e 
è tale che:
Ovvero il prodotto scalare fra 2 vettori non cambia se a entrambi viene applicato lo stesso operatore unitario. Possiamo quindi dire che gli operatori unitari sono nello spazio di Hilbert l’analogo delle rotazioni nello spazio reale a 2 dimensioni.
Si noti che anche l’evoluzione dello stato quantistico è deterministica, come per il caso classico, però in meccanica quantistica l’assegnazione dei valori alle osservabili non è deterministica, ma è data dalla (10).