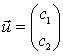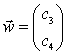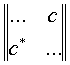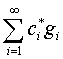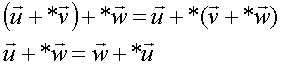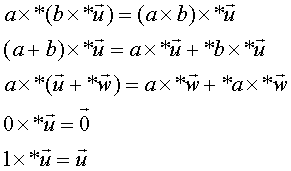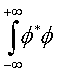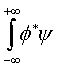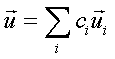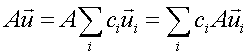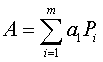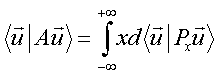I. LA MATEMATICA
Stern e Gerlach nel 1921 produssero un sottile raggio di atomi di argento. Lo fecero passare attraverso i poli di un magnete e osservarono che il raggio veniva diviso in 2 - uno deviato in su e l’altro in giù - che andavano a incontrare in punti diversi un vetro posto dopo il magnete.
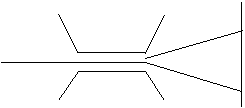
Una spiegazione di questo comportamento potrebbe essere che
gli atomi di argento abbiano agito come dei piccoli magneti che si sono
allineati alla non uniformità del campo del magnete, come dei minuscoli aghi di
bussola. Se così fosse però, gli atomi entrerebbero con un orientamento casuale
del loro momento magnetico, quelli allineati col campo magnetico (paralleli)
dovrebbero andare tutti nella stessa direzione, alcuni dovrebbero avviarsi nella
direzione opposta (antiparallela) e altri arrivare con direzioni intermedie,
formando cioè nom 2 macchie localizzate sullo specchio, ma una striscia
continua.
Si potrebbe allora pensare che gli atomi di argento abbiano
un momento magnetico orientato verticalmente rispetto al campo del magnete, o
in su o in giù. Ma neanche questo funziona, perché, se ruotiamo il magnete di
90° il raggio di atomi si divide ancora in due, ma, invece di andare in su e in
giù, uno va a destra e l’altro a sinistra. Allora gli atomi dovrebbero avere
anche un momento magnetico orizzontale
rispetto al campo del magnete.
Nel 1925 Goudsmit a Uhlenbeck proposero la seguente
spiegazione. Ogni elettrone di un atomo è dotato di un momento magnetico,
chiamato spin, che può avere solo 2 valori:
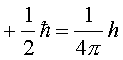e 
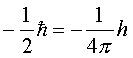
Dove h è la costante di Planck. L’atomo di argento ha 47 elettroni, 46 dei quali hanno spin che si annullano fra di loro. L’elettrone rimasto può avere nella direzione verticale al campo del magnete spin su o spin giù. Questo spiega le due macchie verticali sullo specchio. Lo spin avrà anche una componente orizzontale, che può avere solo 2 valori, che spiega le due macchie sul vetro a destra e a sinistra quando il magnete viene ruotato di 90°.
Mettiamo alla prova questa ipotesi. Facciamo passare un raggio di atomi di argento attraverso un magnete orientato verticalmente. Esso si dividerà in due raggi, uno diretto in su, l’altro in giù. Facciamo poi passare il raggio in su attraverso un magnete orientato orizzontalmente. Il raggio si dividerà ancora in due, uno a destra e l’altro a sinistra. Consideriamo quest’ultimo raggio. Gli atomi di cui è composto hanno una componente verticale dello spin diretta in su e una orizzontale diretta a sinistra. Allora, se noi facciamo passare il raggio per un terzo magnete orientato verticalmente esso non si dovrebbe dividere. Invece esso si divide in due esattamente come con il primo magnete verticale.
Questo fenomeno sfida la nostra capacità di comprensione. Sembra quasi che la divisione del raggio con il magnete orizzontale abbia modificato la componente verticale dello spin. Ma, ancora più strano, solo alcuni degli elettroni hanno subito questa modificazione!
Dopo la scoperta delle linee spettroscopiche di emissione degli atomi, spiegate dal modello semi-quantistico dell’atomo proposto da Bohr, questo è stato il primo fenomeno quantistico osservato.
Esso si spiega con il fatto che lo spin non è una proprietà in senso classico, ma una distribuzione probabilistica. Per rappresentare eventi fisici essenzialmente probabilistici occorre introdurre un formalismo matematico idoneo.
Vettori
Consideriamo i punti di un piano, come quello di questa pagina, i quali possono essere messi in corrispondenza con coppie di numeri reali (x,y). Facciamo corrispondere a un punto la coppia (0,0) e prendiamo un altro punto del piano (x1,y1), dove x1 e y1 sono misurati rispetto a un sistema di coordinate perpendicolari che hanno origine nel punto (0,0). Possiamo tracciare un segmento fra i 2 punti attribuendogli come direzione quella che va dal punto (0,0) verso il punto (x1,y1).
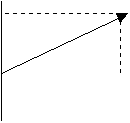
(x1,y1)
(0,0)
Tale segmento dotato di direzione è un vettore e, applicando il teorema di Pitagora, avrà lunghezza o norma:
Un vettore può venir rappresentato in diversi sistemi di coordinate o basi.
E’ importante osservare che la lunghezza di un vettore è indipendente dal sistema di coordinate perpendicolari in cui viene calcolata. Questo fa sì che i vettori sono adatti a rappresentare le forze fisiche, che agiscono in un punto e hanno direzione e intensità. Infatti, se facciamo corrispondere l’intensità della forza alla lunghezza del vettore, essa sarà indipendente dal sistema di coordinate in cui viene rappresentata.
Si può definire la somma fra vettori. Se:
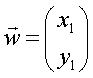e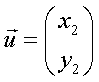 
allora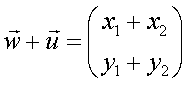 
Che si può rappresentare geometricamente con la regola del parallelogrammo:
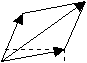
Dalla figura si vede anche che le componenti del vettore somma sono uguali alla somma delle componenti dei 2 vettori sommati.
Si può definire anche il prodotto di un vettore per un numero (uno scalare). Se:
allora 
dove c è un qualsiasi numero reale. La moltiplicazione di un vettore per uno scalare non fa altro che allungare il vettore se c>1, mantenerlo identico se c=1, e accorciarlo se c<1, cambiarlo di verso se c<05.
Operatori
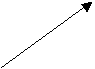
Gli operatori sono enti matematici che agiscono sui vettori trasformandoli. Ad esempio, possiamo definire l’operatore Rq che ruota un vettore di un angolo q. Indicheremo così il vettore risultante dalla rotazione:
Ovvero il vettore 
risulta
dall’applicazione dell’operatore Rq
al vettore 
.
q
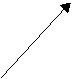
L’operatore che ruota conserva la lunghezza del vettore a cui viene applicato. Esistono anche operatori che non conservano la lunghezza del vettore a cui vengono applicati, come ad esempio i proiettori, che sono molto importanti per la meccanica quantistica. Possiamo definire un proiettore Px che proietta tutti i vettori sull’asse delle x, come nella figura:
Possiamo anche applicare 2
operatori consecutivamente allo stesso vettore. Il risultato della prima
trasformazione sarà un vettore a cui applicheremo la seconda. Con 
indichiamo
l’applicazione prima dell’operatore B e poi dell’operatore A al
vettore 
. AB è detto anche il prodotto dei due
operatori B e A. Si noti che l’applicazione consecutiva di due
operatori non è detto che goda della proprietà commutativa. Ovvero può essere
che il risultato di AB
sia diverso da quello di BA
. Ad esempio se prima ruotiamo un vettore di un angolo q
maggiore di 0 e poi lo proiettiamo sull’asse x otteniamo in generale un
risultato diverso che se prima lo proiettiamo e poi lo ruotiamo. Questo diventa
chiaro se si tiene presente che la proiezione sull’asse x porta
necessariamente a un vettore che giace su quell’asse.
Si dice che un operatore A
è lineare quando per ogni coppia di vettori 
e per ogni numero reale c valgono le 2 seguenti
proprietà:
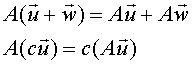(1)
Se nello spazio a 2 dimensioni i vettori possono essere rappresentati da una coppia di numeri reali, tutti gli operatori lineari e solo quelli possono essere rappresentati da una quadrupla di numeri reali, chiamata matrice 2 per 2. L’applicazione di un operatore lineare a un vettore si indica e si calcola così:
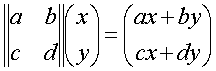
Per eseguire l’operazione si immagini di ruotare di 90° la riga superiore e metterla accanto al vettore, quindi eseguire la somma dei prodotti ax e by. Lo stesso va fatto con la riga inferiore.
Tutti gli operatori di cui ci occuperemo sono lineari e quindi rappresentabili da una matrice.
L’operatore Px che proietta sull’asse x ha una semplice rappresentazione matriciale:
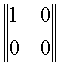
Preso un angolo q si può calcolare il suo seno e il suo coseno tracciando una perpendicolare di fronte all’angolo:
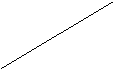Q
q
O P
Allora:
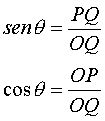
Come d’uso indichiamo:
Angolo retto=90°=
; Angolo piatto=180°=p; Angolo giro=360°=2p
Dove p è il numero 3.14…., cioè il rapporto fra la circonferenza e il diametro di un cerchio.
Come si vede dalla figura, avremo che:
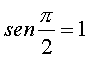
in quanto PQ collassa su OQ. E
Analogamente:
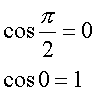
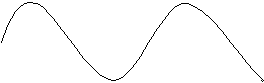
E’ facile vedere che la funzione y=senx ha la seguente rappresentazione geometrica:
In pratica tra 0 e 2p si
svolge un ciclo che si ripete fra 2p e 4p e così via all’infinito. Questo succede perché dopo 2p,
cioè l’angolo giro, gli angoli tornano su se stessi. Il comportamento del
coseno è analogo anche se sfasato di 
.
Per questo le funzioni come il seno e il coseno vengono chiamate periodiche. Esse sono utili a rappresentare dei fenomeni fisici, come le oscillazioni di un pendolo, le vibrazioni di una corda, o le creste e le valli di un’onda.
Infine, dato qualsiasi angolo q, applicando il teorema di Pitagora, si vede subito che:
(2)
Questa breve digressione ci serve, perché l’operatore Rq che ruota un vettore dell’angolo q ha una semplice rappresentazione matriciale in termini di seni e coseni:
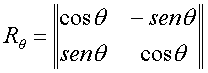(3)
Possiamo anche definire l’operatore identità I, che lascia i vettori invariati. Esso sarà rappresentato dalla matrice:
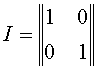
Il prodotto di 2 operatori può essere così rappresentato e calcolato dal prodotto di 2 matrici:
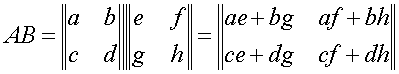
Si noti che il prodotto fra 2 matrici non è la semplice moltiplicazione in serie dei 4 numeri, ma, per così dire, li mescola. Infatti, come abbiamo già detto, il prodotto fra operatori, e quindi anche quello fra matrici, non è commutativo. Ora è facile vedere che:
Cioè la composizione di una proiezione e una rotazione non è commutativa.
Infine sono molto naturali le definizioni della somma di 2 matrici/operatori e la moltiplicazione di uno scalare per una matrice/operatore:
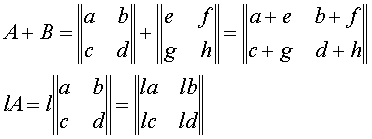
Autovettori e autovalori
Prendiamo l’operatore rappresentato dalla matrice:
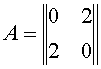
e il vettore
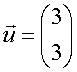
E’ facile vedere che:
Dato l’operatore A, questo vale per qualsiasi vettore della forma
Ma in generale non vale per altri vettori a cui può essere applicato A.
Analogamente per il vettore:
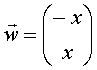
vale:
Sulla base di questo esempio, possiamo dare la seguente definizione:
Si dice che 
è un autovettore
dell’operatore lineare A con il corrispondente autovalore a
se 
e 
.
In pratica gli autovettori di un operatore lineare indicano geometricamente quelle linee o direzioni tali che l’applicazione di quell’operatore a un vettore che giace lungo una di quelle direzioni non fa altro che moltiplicare il vettore per un numero. Tale numero è il corrispondente autovalore.
Non tutti gli operatori hanno autovettori. Ad esempio le rotazioni non possono avere autovettori per ovvi motivi geometrici. Per contro, i proiettori hanno come autovettori l’asse su cui proiettano e quella perpendicolare a essa. Una classe importante di operatori è quella che ha autovettori perpendicolari (ortogonali) fra loro. Essi sono gli operatori simmetrici, che vengono rappresentati da una matrice che ha gli elementi che non stanno sulla diagonale da sinistra a destra uguali 2 a 2:
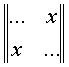
Prendiamo un operatore simmetrico A, che ammette 2 autovettori a cui corrispondono 2 autovalori diversi a1 e a2. Allora esisteranno 2 rette L1 e L2 ortogonali fra loro su cui giacciono questi autovettori. Ci saranno anche 2 operatori di proiezione P1 e P2 che proietteranno su queste rette. Si può allora dimostrare che vale il seguente teorema, detto anche della scomposizione spettrale:
Cioè ogni operatore simmetrico è esprimibile come una combinazione lineare dei suoi autovalori moltiplicati per i proiettori sulle linee definite dai corrispondenti autovettori.
Quando gli autovalori di A sono uguali, allora tutti i vettori sono autovettori di A e la scomposizione vale per qualsiasi coppia di proiettori su direzioni ortogonali.
Come vedremo, il teorema di scomposizione spettrale è molto importante per il formalismo della meccanica quantistica.
Il prodotto scalare fra vettori
Indichiamo il prodotto scalare (inner o dot product) fra 2 vettori con la notazione introdotta da Dirac; esso viene così definito:
Se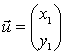 
e 
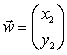allora il prodotto
scalare 
.
Il prodotto scalare di 2 vettori è un numero e non un vettore. Si noti che:
E siccome 
sono i quadrati delle
componenti del vettore 
, il prodotto scalare di un vettore per se stesso
rappresenta, per il teorema di Pitagora, il quadrato della lunghezza del
vettore. Indichiamo la lunghezza del vettore 
con 
:
Un vettore che ha lunghezza uguale a 1 si dice normalizzato.
Si può dimostrare che:
(4)
Ovvero che il prodotto scalare fra 2 vettori è uguale al prodotto delle loro lunghezze per il coseno dell’angolo che formano. Questo significa che il prodotto scalare, così come la lunghezza di un vettore, è indipendente dalle coordinate che si sono scelte.
Due vettori ortogonali fra loro
formano un angolo pari a 
; il coseno di un angolo retto è uguale a 0, per cui il
prodotto scalare di 2 vettori ortogonali è 0.
Consideriamo un vettore
normalizzato 
e una retta L
che forma un angolo f
con 
. Se P è il proiettore sulla retta L, allora si
può dimostrare che vale:
(5)
Siccome il coseno di un angolo
varia fra 0 e 1, anche l’espressione 
varierà nello stesso
intervallo. Vedremo che questa espressione è legata alle probabilità in
meccanica quantistica.
Inoltre, se P1 e P2 sono proiettori su 2 rette fra loro ortogonali, vale:
Quindi le 2 espressioni 
e 
potrebbero essere le
probabilità di 2 eventi tra loro alternativi e complementari.
I numeri complessi
Finora abbiamo parlato dei vettori e delle loro relazioni geometriche con riferimento ai numeri reali. Possiamo ora introdurre i numeri complessi, che arricchiscono la capacità rappresentativa della matematica.
Consideriamo l’equazione:
Essa non ha alcuna soluzione nell’ambito dei numeri reali. Definiamo allora un nuovo numero i e vediamo che proprietà avrà:
Possiamo formare un nuovo insieme di numeri del tipo ri dove r è un qualsiasi numero reale. Questi numeri, detti immaginari, possono essere facilmente sommati e sottratti fra loro. Si noti però che:
In quanto (i)(i)=-1.
Possiamo anche sommare un numero immaginario con un numero reale s, ottenendo un numero complesso della forma ri+s. Si osservi che questa espressione non è ulteriormente riducibile, per cui, in un certo senso, un numero complesso è in grado di portare l’informazione di 2 numeri reali, ad esempio l’individuazione di un punto del piano.
La somma e la moltiplicazione di 2 numeri complessi si definiscono in modo molto naturale:
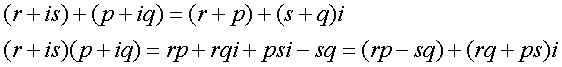
Molto importante è la definizione
del modulo di un numero complesso c=r+si, che si indica 
:
Se 
allora 
. Per la (2) esisterà un angolo q tale che:
cosq cosq+isenq
q
(6)
Se 
e 
allora 
Allora quasi tutto ciò che abbiamo
detto in precedenza per il caso a 2 dimensioni vale senza problemi. Però il
prodotto scalare diventa una somma infinita. Consideriamo i vettori 
e 
, allora sarà:
(7)
Noi considereremo solo degli spazi
in cui per qualsiasi coppia di vettori questa sommatoria ha un valore finito.
Tenendo conto che la lunghezza di un vettore 
è data da 
, in questi spazi tutti i vettori hanno lunghezza finita.
Inoltre esiste un vettore 
che chiamiamo
elemento neutro tale che:
(8)
1. se 
e 
appartengono a L,
anche 
appartiene a L;
2. se 
appartiene a L
anche a
appartiene a L, dove a è un qualsiasi scalare.
Una coppia di vettori normalizzati
e ortogonali fra loro può generare qualsiasi punto del piano per combinazione
lineare. Possiamo generalizzare questa nozione. Una serie di vettori 
è detta una base
ortonormale dello spazio vettoriale V, se ogni vettore 
di V può
essere generato come combinazione lineare del tipo 
e tutti i vettori
della base sono ortogonali fra loro e normalizzati.
E’ importante il seguente teorema.
Preso un qualsiasi operatore lineare A che agisce nello spazio
vettoriale V e una qualsiasi base ortonormale 
dello spazio
vettoriale V, poiché un qualsiasi vettore 
potrà essere espresso
come:
Sia A un operatore
hermitiano su uno spazio vettoriale V a dimensione finita. Allora ci
sono numeri reali 
e proiettori 
(m£n),
che proiettano su sottospazi fra loro ortogonali di V tali che:
Quando uno spazio vettoriale ha
infinite dimensioni non tutti gli operatori hermitiani a spettro continuo hanno
autovalori. Fra questi alcuni sono molto importanti per la meccanica
quantistica, come ad esempio quelli che rappresentano la posizione Q e
il momento P. Anche per essi si può formulare il teorema di
scomposizione spettrale, ma richiede della matematica assai più complessa.
Possiamo rendere l’idea nella seguente maniera. Invece di considerare 
, consideriamo il prodotto scalare 
, dove A è hermitiano su uno spazio vettoriale a
infinite dimensioni. Ora consideriamo un insieme continuo di numeri reali 
. Per un operatore hermitiano è possibile trovare una
famiglia di operatori di proiezione Px, tali che se indichiamo
con 
la variazione
infinitesima di questo prodotto scalare che avviene in corrispondenza di un
valore di x, allora:
Dato questo teorema è possibile
associare a ogni intervallo semi-chiuso di numeri reali 
un proiettore 
.
