IV. STATI MISTI E SISTEMI COMPOSTI

Operatori della classe traccia

Si dice che un operatore è positivo su uno spazio H quando per tutti i vettori di H il suo valore di aspettazione è maggiore o uguale a 0. Se A è positivo, si può dimostrare che è hermitiano. Si consideri una base ortonormale dello spazio H. Si dice che un operatore A appartiene alla classe traccia se A è positivo e è finita. Si può dimostrare che il valore di è indipendente dalla base prescelta. Possiamo allora definire così la traccia di un operatore:

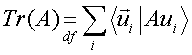
Proviamo a calcolare la traccia di un operatore di proiezione P su un sottospazio unidimensionale. Scegliamo una base ortonormale che abbia un vettore che giace nel sottospazio su cui proietta P e gli altri tutti ortogonali a . Allora avremo che:

Per cui:

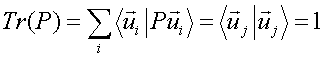
Si può dimostrare che la traccia di un operatore di proiezione che proietta su un sottospazio di dimensione n è uguale a n.

Se A è della classe traccia e non ha autovalori degeneri, allora, usando il teorema di scomposizione spettrale:

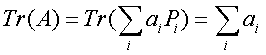(16)

In altre parole, la traccia di A è uguale alla somma dei suoi autovalori. Nella rappresentazione matriciale, la traccia di A è la somma dei suoi elementi diagonali. Valgono inoltre le seguenti uguaglianze:

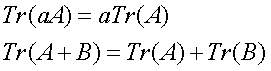(17)

Operatorii densità

Quando un operatore D è della classe traccia e Tr(D)=1 si dice che D è un operatore densità. Chiaramente ogni proiettore P che proietta su un raggio è un operatore densità.

Consideriamo una famiglia di proiettori P_i che proiettano su raggi dello spazio H. Allora, per le (17):

è un operatore densità se ogni a_i è maggiore o uguale a 0 e .

Si può dimostrare che ogni operatore densità D ha autovalori b_i compresi fra 0 e 1. Per la (16), la loro somma è uguale a 1. E, quindi, per il teorema di scomposizione spettrale si può scrivere D come:

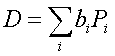
Dove i P_i proiettano su raggi tra loro ortogonali.

Se D non è un operatore di proiezione, allora esso è esprimibile in un numero infinito di modi come somma pesata di proiettori su raggi non necessariamente ortogonali fra loro.

In uno spazio H, prendiamo un operatore di proiezione su un raggio che contiene il vettore normalizzato e un qualsiasi altro operatore di proiezione P. Scegliamo una base ortonormale che contiene . Allora e se risulta . Si consideri la quantità . Si può dimostrare che è uguale a . Quindi:

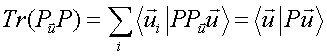(18)

Questo significa che la quantità agisce esattamente come l’algoritmo statistico della meccanica quantistica rispetto al vettore di stato . In altre parole, utilizzando la (18), possiamo esprimere la (9) mettendo al posto di un vettore di stato il corrispondente proiettore sul raggio individuato da quel vettore. Cioè:

Sappiamo che un operatore densità è esprimibile come una somma pesata di proiettori tali che la somma dei coefficienti dà 1. Essi quindi sono adatti a esprimere una misura di probabilità sull’insieme di sottospazi che corrispondono ai proiettori:

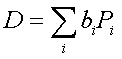
Per cui, per la (18):

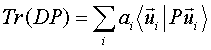
dove è un vettore del sottospazio su cui proietta P_i. Quindi, se sostituiamo a un operatore densità nell’espressione otteniamo una misura di probabilità sui possibili vettori di stato .

Consideriamo l’osservabile A con autovalori discreti esprimibile per il teorema di scomposizione spettrale come:

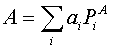
Ne segue che se rappresenta la domanda sperimentale “l’osservabile A ha un valore compreso nell’intervallo D”, abbiamo che:

(19)

Cioè la quantità fornisce la probabilità che l’osservabile A abbia un valore compreso nell’intervallo D premesso che il vettore di stato può essere uno dei possibili espressi dall’operatore densità D.

La (19) fornisce una rappresentazione matematica dell’algoritmo statistico per gli stati misti, intesi come insiemi probabilisticamente pesati di stati puri. Abbiamo detto in precedenza che le probabilità che compaiono negli stati misti possono essere interpretate come forme di ignoranza, a differenza di quelle che compaiono negli stati puri. Tuttavia questa interpretazione incontra un limite. Abbiamo visto sopra che la scomposizione di un operatore densità in una somma pesata di proiettori non necessariamente ortogonali non è unica. Quindi lo stesso operatore densità può fornire indifferentemente diverse probabilità per lo stesso stato puro. A volte però questa indeterminazione viene eliminata dal tipo di preparazione sperimentale.

In conclusione l’operatore densità è una generalizzazione del concetto di stato.

Il teorema di Gleason

Consideriamo l’insieme S dei possibili sottospazi di uno spazio H. Una funzione m che va da S ai numeri reali positivi sarà una misura su S se:

1. allora

2. , tutti gli L_i sono disgiunti fra loro e la loro unione è uguale a L, allora

3. La misura dell’insieme vuoto è uguale a 0.

Il concetto di misura è intuitivo. Una misura assegna un numero reale a un sottospazio, in modo che a sottospazi più comprensivi corrisponda un numero più grande, allo spazio vuoto corrisponda lo 0 e all’unione di sottospazi corrisponda la somma delle loro misure. E’ chiaro che la funzione misura è un concetto utile a trattare il passaggio dallo spazio degli stati ai risultati possibili di una misurazione.

Uno spazio H si dice separabile, se contiene un sottoinsieme di sottospazi che è denso, cioè con la potenza dei numeri razionali.

Intuitivamente un sottospazio L di uno spazio H si dice chiuso quando contiene la sua frontiera.

Possiamo ora enunciare un teorema dimostrato da Gleason nel 1957 che riveste una certa importanza per i fondamenti della meccanica quantistica.

Sia m una misura sui sottospazi chiusi di uno spazio di Hilbert separabile H di dimensione maggiore o uguale a 3 tale che m(H)=1. Allora esiste un operatore hermitiano T tale che Tr(T)=1, e per tutti i sottospazi L chiusi di H vale:

In altre parole, se lo spazio di Hilbert ha almeno 3 dimensioni, allora qualsiasi misura di probabilità è rappresentabile da un operatore densità.

Vedremo più avanti per quali ragioni il teorema di Gleason impedisce certe forme di completamento della meccanica quantistica.

Sistemi composti e prodotto tensore

Se 2 sistemi quantistici vengono considerati come parti di uno stesso sistema e ognuno è rappresentato rispettivamente da un vettore negli spazi di Hilbert H_a e H_b, allora lo stato del sistema composto e le sue osservabili saranno rappresentate in uno spazio H_aÄH_b chiamato prodotto tensore di H_a e H_b. Esso viene costruito in modo che se è una base ortonormale per H_a e è una base ortonormale per H_b, allora l’insieme di coppie - che indichiamo con sarà la base ortonormale di H_aÄH_b.

Non entriamo nei dettagli della costruzione dello spazio prodotto tensore; notiamo però una sua caratteristica sorprendente. L’insieme di tutti i vettori esprimibili nella forma è un sottoinsieme proprio – cioè non uguale all’intero – di H_aÄH_b. Ovvero, sebbene ogni vettore dello spazio H_aÄH_b è una somma lineare di vettori esprimibili nella forma , non ogni vettore dello spazio è esprimibile direttamente nella forma . In questo senso il prodotto tensoriale è diverso dal prodotto cartesiano.

Questo fatto ha delle conseguenze importanti.

Sia D un operatore densità sullo spazio H_aÄH_b, che rappresenta lo stato di un sistema composto. Assumiamo che la scomposizione spettrale di 2 operatori hermitiani A_a e A_b rispettivamente negli spazi H_a e H_b sia data dagli insiemi di proiettori P^a e P^b. Ci chiediamo, esistono stati (operatori densità) D_a e D_b dei sistemi componenti che per tutte le osservabili A_a e A_b e per tutti gli intervalli D e G di numeri reali soddisfano le seguenti equazioni?

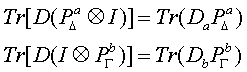(20)

Cioè esistono degli stati (operatori densità) dei sistemi componenti che riproducono le probabilità del sistema composto che si trova nello stato D? L’uso dell’operatore identità nella parte sinistra delle 2 equazioni sta a indicare che ci interessano solo i risultati riguardanti una parte del sistema composto rappresentato da D.

Enunciamo la risposta a tale quesito senza dimostrarla.

1. Se i 2 sistemi componenti si trovano in uno stato puro, allora esiste un solo stato puro che rispetta le (20).

2. Se il sistema composto si trova in uno stato puro, allora esso definisce univocamente gli stati componenti che rispettano le (20). Tuttavia gli stati componenti saranno puri solo se lo stato composto è esprimibile nella forma , altrimenti sono misti. Questo pone dei problemi all’interpretazione delle probabilità che compaiono negli stati misti come forme di ignoranza. Infatti sulla base di questa interpretazione, se i sistemi componenti si trovano in uno stato misto anche quello composto dovrebbe trovarsi in uno stato misto.

3. Se lo stato del sistema composto è misto, allora esso definisce univocamente gli stati misti dei sistemi componenti che rispettano le (20).

4. Se gli stati dei sistemi componenti sono misti, allora il sistema composto che rispetta le (20) non è definibile univocamente, potrebbe anche essere uno stato puro.

In generale, uno stato definito nello spazio prodotto tensore è più ricco di informazioni degli stati nei singoli spazi.